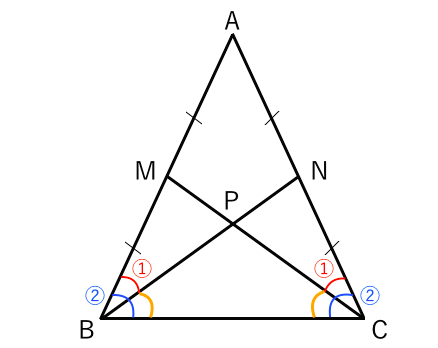
定理6 ABCは正三角形でない、 ab=acの二等辺三角形で、 その内部の点pが、 acの垂直二等分線上にある すなわち、 am=mc、ac⊥pm かつ、∠abp=頂角bacの 半分を満たすならば、apは 頂角bacの二等分線上にある。 証明 頂角bac=2a 、acとabの中点二等辺三角形の性質 名前 図の abcが二等辺三角形のとき、( )に当てはまる 言葉を書きなさい。 ①∠aを ( ) という。 ②∠b,∠cを( )という。 ③( )が等しい三角形を二等辺三角形 b c という。←二等辺三角形の定義 二等辺三角形の定理Dec 21, 14 · 二等辺三角形の性質(定理)である「二等辺三角形の頂角の二等分線は底辺を垂直に2等分する。」がありますが、逆に「二等辺三角形の底辺を垂直に2等分した線分は頂角を二等分する。」っていえますか?質問の命題は言えます。でも、これ
My Math Note
二等辺三角形の定理 証明
二等辺三角形の定理 証明-Feb 19, 21 · 直角二等辺三角形は、重要な特徴をもった図形なので、問題を解くときに大きなヒントとなることが多いです。 今までに習った「直角三角形」と「二等辺三角形」についてもきちんと理解しておきましょうね。 直角三角形とは?Sep 12, 18 · 世界に1つだけの三角形の組 -抽象現代数学を駆使して素朴な定理の証明に成功- 慶應義塾大学大学院理工学研究科KiPAS数論幾何グループの平川義之輔(博士課程3年)と松村英樹(博士課程2年)は、『辺の長さが全て整数となる直角三角形と二等辺三角形
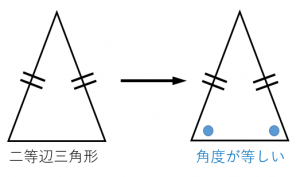



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学
二等辺三角形の定理 by 蛭子井博孝 hi by H.E 06 hiる二等辺三角形dar ができます。 ad=af であるから、 adr と afq は同じ形 であり、∠raq=60°でもあるので、 arq は正三角形となることがわかりますね。 rq は辺bc と平行ですから、 erq も adr や afq と同じ形の二等辺三角形であることも確認 できます。(証明) 1 右のようにACが中心を通るとき oc=ob= (半径)だから OBCは二等辺三角形になる. 二等辺三角形の2つの底角は等しいから ∠ b= ∠ c (1) 「三角形の外角は,それと隣り合わない2つの内角の和に等しい」(重要定理)から,
初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理(さんへいほうのていり)、勾股弦の定理(こうSep 03, 18 · 二等辺三角形の定理 定理 二等辺三角形の性質 二等辺三角形の2つの底角は等しい。 二等辺三角形の頂角の二等分線 二等辺三角形の頂角の二等分線は,底辺を垂直に2等分する。 2つの角が等しい三角形 2つの角が等しい三角形は二等辺三角形である。直線OA、OP、OBは円の半径なので, OA=OP=OB OA=OPだから、⊿OPAは二等辺三角形。 二等辺三角形の底角は等しいので、 ∠OAP=∠OPA=∠a とおく。 三角形の外角の定理より
直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。 直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。A三平方の定理(ピタゴラスの定理) 直角三角形の直角をはさむ2 辺の長さをa,bとし,斜辺の 長さをcとすると a2 +b2 =c2 が成り立つ。これを三平方の定理(ピタゴラスの定理)という。 直角三角形の辺の2点間の距離の公式を用いて三角形の種類(二等辺三角形,直角三角形など)を求めるためには, 1 まず,三辺(AB,BC,CAなど)の長さを求めます. 2 次に, (1) 「AB=BC」 ならば 「AB=BCの二等辺三角形」などと答えます.
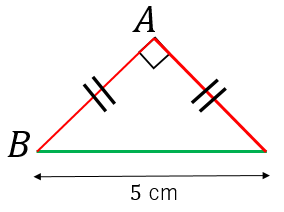



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく
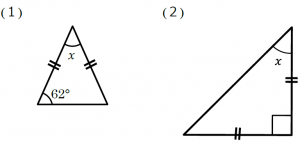
(三角形の角の二等分線に関する公式2) (証明) CからADに平行な直線を引き、Abとの交点をEとする。 よって、 ACEは二等辺三角形、AE=AC。 ADとECが平行より、AB:AE=BD:DC、 AE=ACだから、AB:AC=BD:DC。14 二等辺三角形の頂点から対辺に伸びる線分 c ad=√ab×ac−bd×dc 15 メネラウスの定理 c ea ab ×bf fc ×cd de =1 16 チェバの定理 c af fb ×bd dc ×ce ea =1 17 ヘロンの公式d 𝑠= 2 (三角形の面積)= 1 2 √ s(−a )b c 18 トレミーの定理 d ac×bd=ad×bcab×dc 19Jul 03, 19 · 二等辺三角形の定理「二等辺三角形の底角は等しい」から、ポイントは二等辺三角形の底角を見つけることです。 ⑴は、1つの底角の大きさが62°なので、もう1つの底角の大きさも62°です。三角形の内角の和が180°(定理)なので、 x=180°−2×62°=56°




二等辺三角形の性質 Youtube



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン
(単に「二等辺三角形」と答えると,どの2辺が等しいのか分かりませんので,等しい2辺も書くようにします.) a 2 =b 2 c 2 などは,辺に関する式から角に関する結論を出すものですが,これは中学校で習う三平方の定理の逆なので,簡単に分かるでしょう.Feb 22, 21 · まずは定理の確認からです。 定理:二等辺三角形の底角は等しい この定理を当然のこととして知っている人も多いと思います。図でも確認しておきましょう。 どこAB =c である正方形や矩形など図形相互の差し引きに還元する頂点 \mathrm{C} から股 AB への垂線 CD =d の足 \mathrm{D} によって,股AB をAD =f とDB =e の二つに分け,左右の 三角形にそれぞれ 「勾股弦の定理」を適用する




数学用語の説明 定義と定理の違いとは 中学数学 定期テスト対策サイト




二等辺三角形の性質と証明 無料で使える中学学習プリント
Feb 19, 21 · 二等辺三角形の定理・性質 二等辺三角形には、\(2\) つの定理(性質)があります。 定理①角度の性質 二等辺三角形の \(2\) つの底角は等しくなります。二等辺三角形の底角(定理) 二等辺三角形の底角が等しいことの証明 ab=acの二等辺三角形abcで∠abc=∠acbを証明する。 a b c 証明 d 頂角bacの二等分線をひき、底辺bcとの交点をdとする。 abdと acdにおいて ∠bad=∠cad(角の二等分線) ab=ac(仮定) ad=ad(共通)May 31, 21 · この性質から二等辺三角形の内角の関係は 頂角(∠A)+底角×2=180° と表せ、つまり内角の角度がどこか1つでもわかれば全部わかるというお得な三角形ということがわかる。




世界に一つだけの 三角形ペア 発見 慶大院生2人証明 朝日新聞デジタル



1
Nov 03, 15 · 二等辺三角形の2つの性質・定理 二等辺三角形には2つの性質があるんだ。 2つの底角は等しい 頂角の二等分線は、底辺を垂直に2等分する二等辺三角形の選択した2つの入力値から他の要素の値を計算します。 入力指定 底辺と高さ 底辺と斜辺 底辺と底角 斜辺と高さ 斜辺と底角 高さと底角 面積と底辺 面積と高さ 面積と斜辺 面積と底角 高さ定理の逆 二等辺三角形 ABC において次のことが成り立っている。 が入れ替わっている。 を入れ替えたものを 逆 という。 ② は ① に逆である。 二等辺三角形である。 正三角形である。 イはアの逆であるがイの文章は正しくない。 二等辺三角形の中には正三角形でないものもたくさんあるからね。




二等辺三角形の角度の問題 基礎から応用までパターン別に解説 中学数学 理科の学習まとめサイト
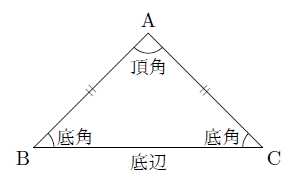



二等辺三角形の性質 まなびの学園
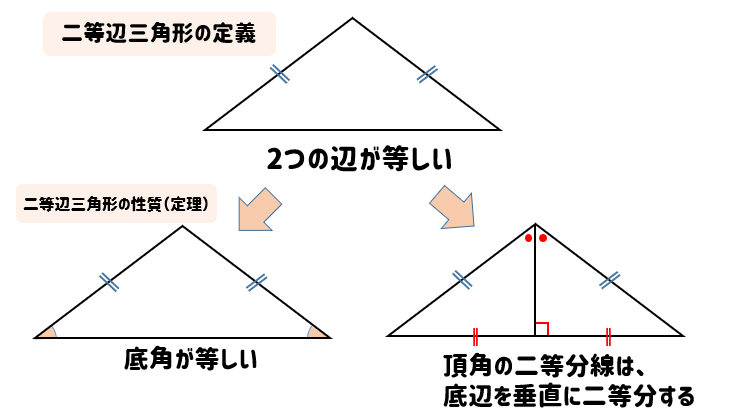
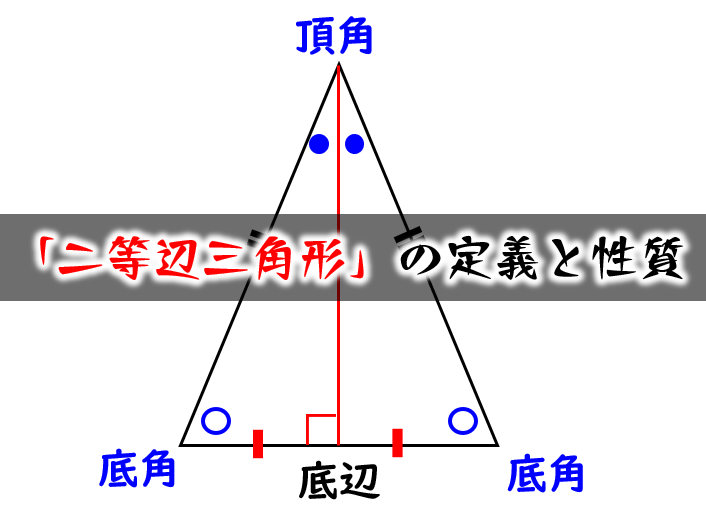
① 二等辺三角形の2つの底角は等しい。 ② 二等辺三角形の頂角の二等分線は底辺を垂直に二等分する。 ③ 二辺の長さが等しい三角形は二等辺三角形である。二等辺三角形の頂角の二等分線は, 底辺を垂直に2 等分する さが等しい 1組の対辺が平行でその長 四角形は、平行四辺形 2つの角が等しい三角形は、その 角を底角とする二等辺三角形 定義 長方形 4つの角がすべて等しい四角形 正三角形 定義3つの辺が等しい三角形二等辺三角形の定義や定理について理解できましたか? これらの二等辺三角形の性質は、当たり前の知識として問題を解く時に問われます。 上の図で言えば、赤くなっているところが 特徴2「頂角の二等分線は、底辺を垂直に二等分する」の該当箇所になっ




二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学



Http Ed City Daito Osaka Jp Weblog Files Tani Jhs Doc 77 3045 Pdf
二等辺三角形の定理を証明したいんだけど! こんにちは!この記事をかいているKenだよ。スープは濃いめに限るね。 二等辺三角形の定理にはつぎの2つがあるよ。 底角は等しい 頂角の二等分線は底辺を垂直に2等分する こいつらって、むちゃくちゃ便利。二等辺三角形の定理1 定義を基にして証明された事柄のうち,よく使われるものを定理といいます。二等辺三角形の2つの底角は等しいです。これは,頂角の二等分線を引いて2つの三角形の合同を示せば得られます。 静止画 e1san3jpg 600×400、 1145KB 中学二等辺三角形の定理② 頂角の二等分線 下の図のようにab=acである二等辺三角形の∠aの二等分線をひき,bcとの交点をdと して,二等辺三角形の性質を調べてみよう。次の にあてはまることば,記号をかきなさい。 ∠ = ∠ = ∠ = ∠ = ∠ = ∠ = ∠




三平方の定理の二等辺三角形の比がありますが それを使うにはその図形の角度が写真のよう Clear



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン
二等辺三角形は、 = となる三角形のことであり、 を頂角、, を底角という。 定理 113 二等辺三角形の底角は等しい。 証明 二等辺三角形を (=) とおこう。このとき、bc の中点を x とおく。Dec 13, · 三平方の定理の証明⑬(外接円と直角二等辺三角形を利用した証明) 年12月13日 中3数学 平面図形 中3数学 三平方の定理にはたくさんの証明方法があります。 今回は外接円と直角二等辺三角形を利用した証明方法について紹介します。 目次 1 Ⅰ 三平合同条件を示すのに二等辺三角形の性質を用いたいからです。 三辺相等の合同の定理は 他の合同条件にくらべて やっかいなのです。 さて、これで 「二辺挟角」「二角挟辺」「三辺相等」という 2つの三角形が合同になるための 3つの定理が出そろいました。




高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ




二等辺三角形の定義と定理 算数 数学が好きになりmath
二等辺三角形になるための条件(1) 二等辺三角形になるための条件 定理 三角形の2つの角が等しければ、その三角形は等しい2つの角を底角 とする二等辺三角形である。 1 下の図のように、AB=ACの二等辺三角形ABCの辺AB,AC上にそれぞれ



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ




三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



Q Tbn And9gcsnbiv 7svsm 6o0qjqco66pmarde4rrmbqkrgwufvawvziomrf Usqp Cau




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ




二等辺三角形の面積を求める算数の公式は



二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明
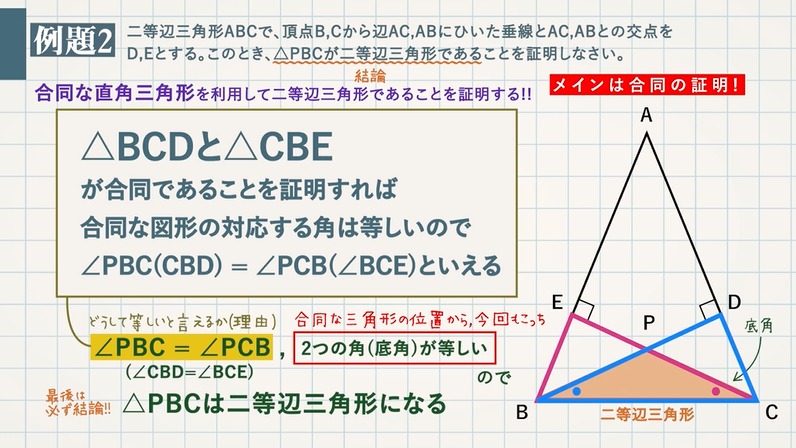



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
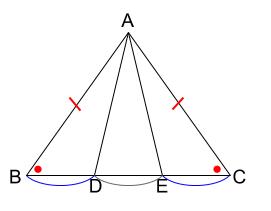



中学数学 証明 二等辺三角形の性質の利用 中学数学の無料オンライン学習サイトchu Su
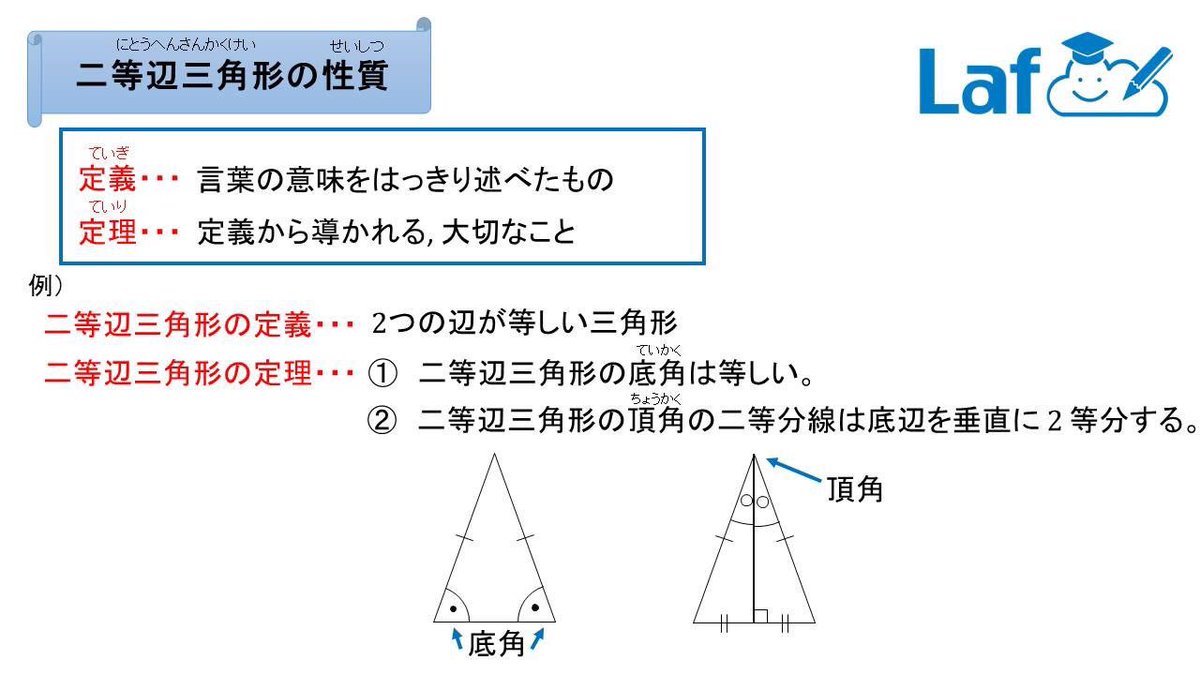



押川 隼也 高校 大学受験対策 على تويتر 中2数学 二等辺三角形の性質 ここでは 定義 と 定理 という小難しい言葉が出てきますね O O 定義 言葉の意味を丁寧に説明したものだよ 二等辺三角形の定義 二つの辺が等しい三角形 定理




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ



1
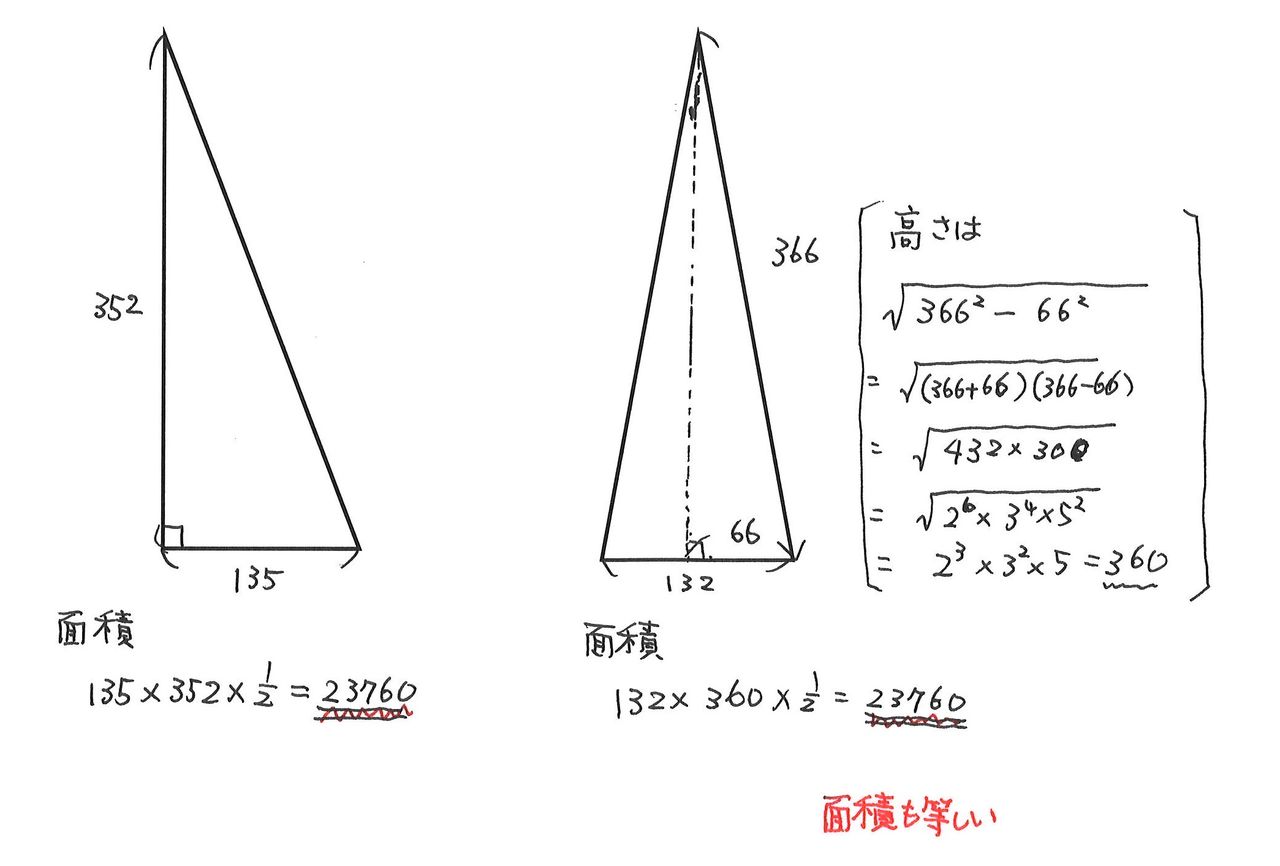



三角形のペア 大田 桐光本部校 ブログ




ม 2 โน ตของ 二等辺三角形 ช น Junior High数学 Clear




二等辺三角形の性質の証明 頂角の二等分線 Youtube




ม 2 โน ตของ 二等辺三角形の性質 ช น Junior High数学 Clear




無料印刷可能直角二等辺三角形 比率 最高のぬりえ




二等辺三角形と正三角形 算数用語集




二等辺三角形の頂角の角度を求めよ 解答編その2 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog
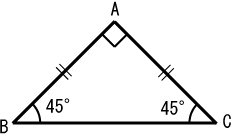



直角二等辺三角形 Wikipedia




二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




簡単公式 二等辺三角形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
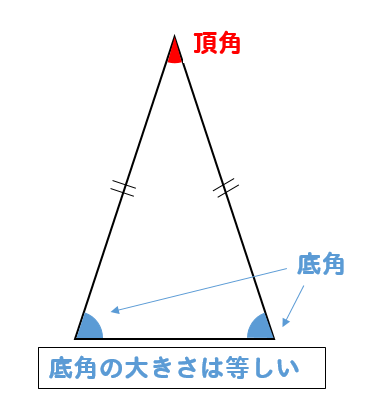



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ
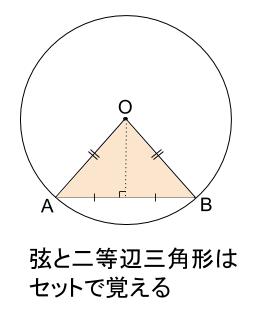



中学数学 三平方の定理 円と接線 弦 中学数学の無料オンライン学習サイトchu Su




中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ
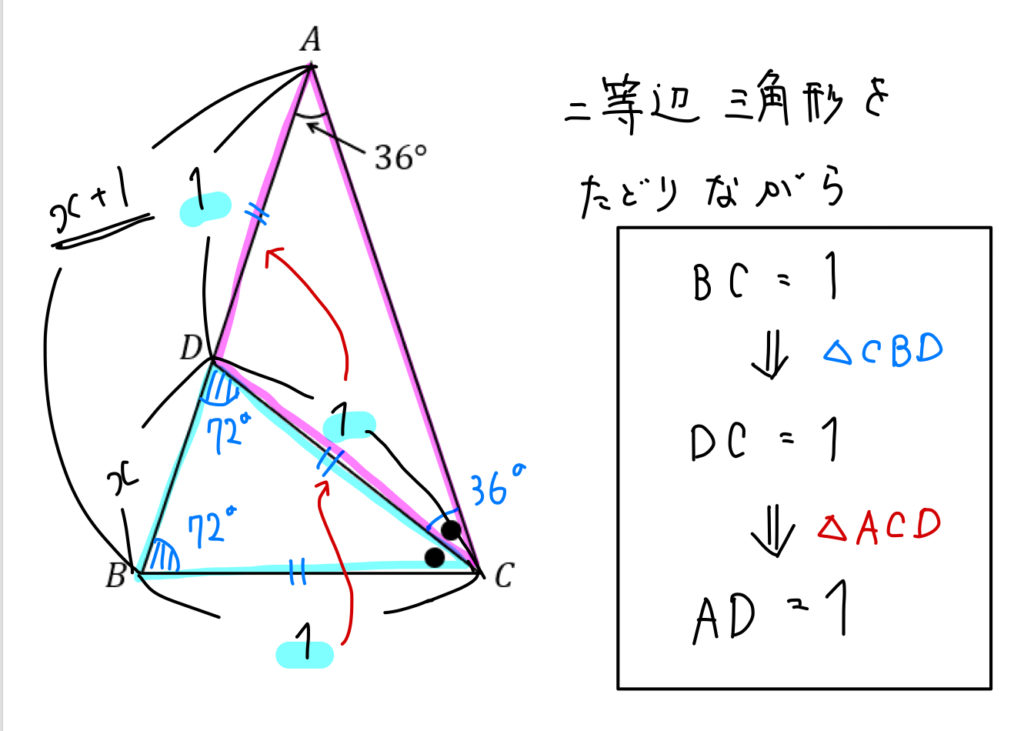



数学 36 の三角比 二等辺三角形を用いて求める方法は 数スタ



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典
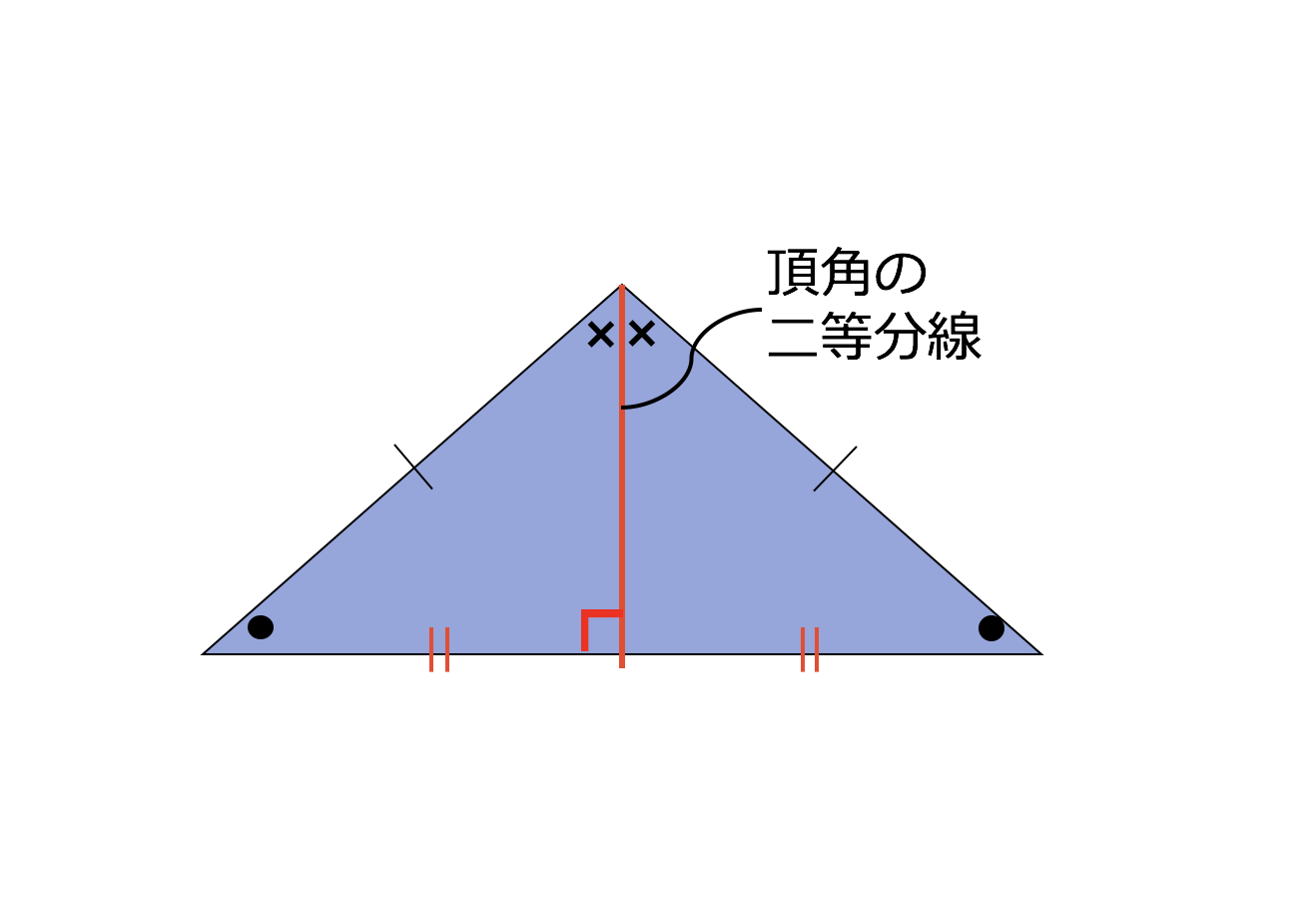



3分で分かる 二等辺三角形の特徴 角度 辺など についてわかりやすく 合格サプリ




直角二等辺三角形の面積を求める公式は 覚えずに自分でつくろう




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ
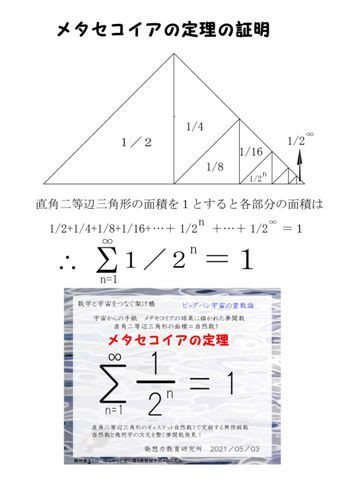



B178fdwaz62h M
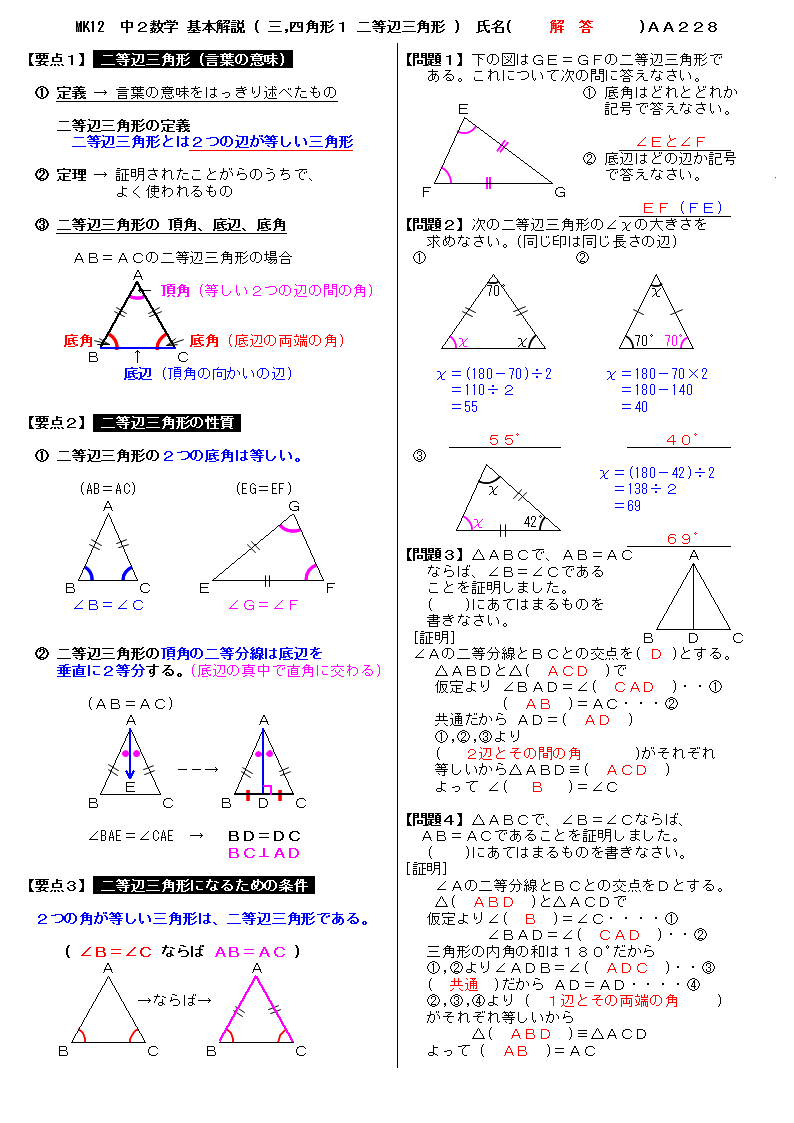



無料 中2数学 基本解説 解答プリント 228 三角形 四角形1 二等辺三角形




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
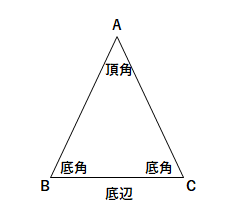



中2数学 二等辺三角形の定義と性質 Examee




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学




二等辺三角形の性質と証明 無料で使える中学学習プリント




二等辺三角形になるための条件 Youtube




3 おかしな不等辺三角形 Imujii S Page



My Math Note




二等辺三角形になることの証明 Youtube
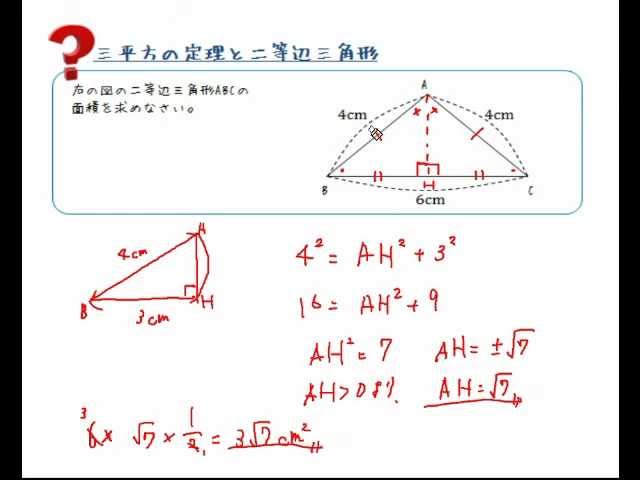



三平方の定理と二等辺三角形 Youtube




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
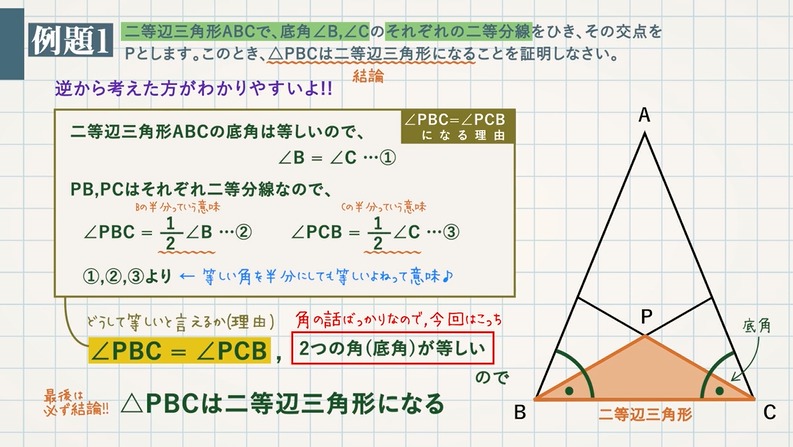



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




二等辺三角形 Wikipedia
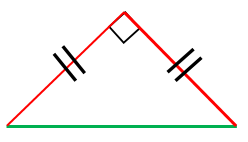



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
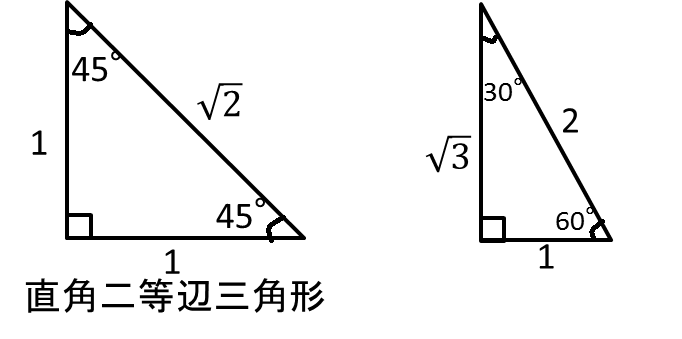



高校受験対策bot 数学 三平方の定理 三平方の定理を習ったら 合わせて覚えておこう 三角定規 90 45 45 1 1 2 直角二等辺三角形 90 60 30 1 2 3 2が斜辺 T Co Rrmbv3lvbw




中2数学 二等辺三角形の性質2 頂角の二等分線 練習編 映像授業のtry It トライイット



1



4 Abccbc Abac Lihat Cara Penyelesaian Di Qanda




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




二等辺三角形の定理や性質 底角が等しいことは絶対に覚えよう 中学や高校の数学の計算問題




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット
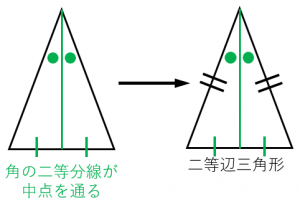



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学



Studydoctor二等辺三角形や台形の面積と三平方の定理 中学3年数学 Studydoctor




今 二等辺三角形が熱い 小学校の算数が懐かしい デイリーポータルz
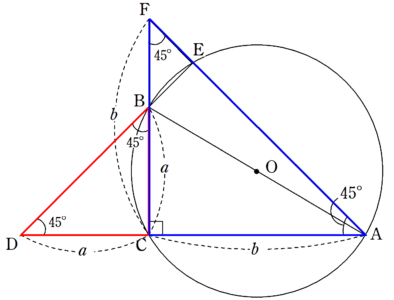



三平方の定理の証明 外接円と直角二等辺三角形を利用した証明 Fukusukeの数学めも



二等辺三角形の定義と性質 問題の解き方 数学fun



二等辺三角形と証明 中学2年 数学クラブ




ม 2 โน ตของ 数学 中2 定義と定理 ช น Junior Clear




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



高校入試 英語 数学 学習 三角形と四角形 二等辺三角形
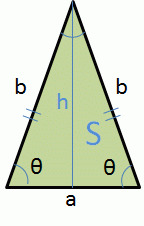



三角形の公式 Wakatta




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典



合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に




頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo




二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4




中2数学 二等辺三角形の性質1 底角が等しい 練習編 映像授業のtry It トライイット




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
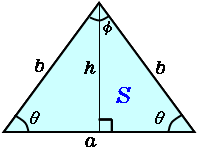



二等辺三角形 高精度計算サイト




働きアリ 三平方の定理




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学
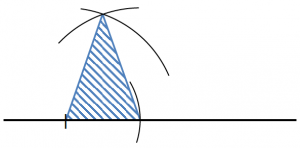



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン




ม 2 โน ตของ 中2 数学 二等辺三角形など ช น Junior Clear




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




辺の長さが全て整数となる直角三角形と二等辺三角形で周の長さも面積も共に等しい組 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
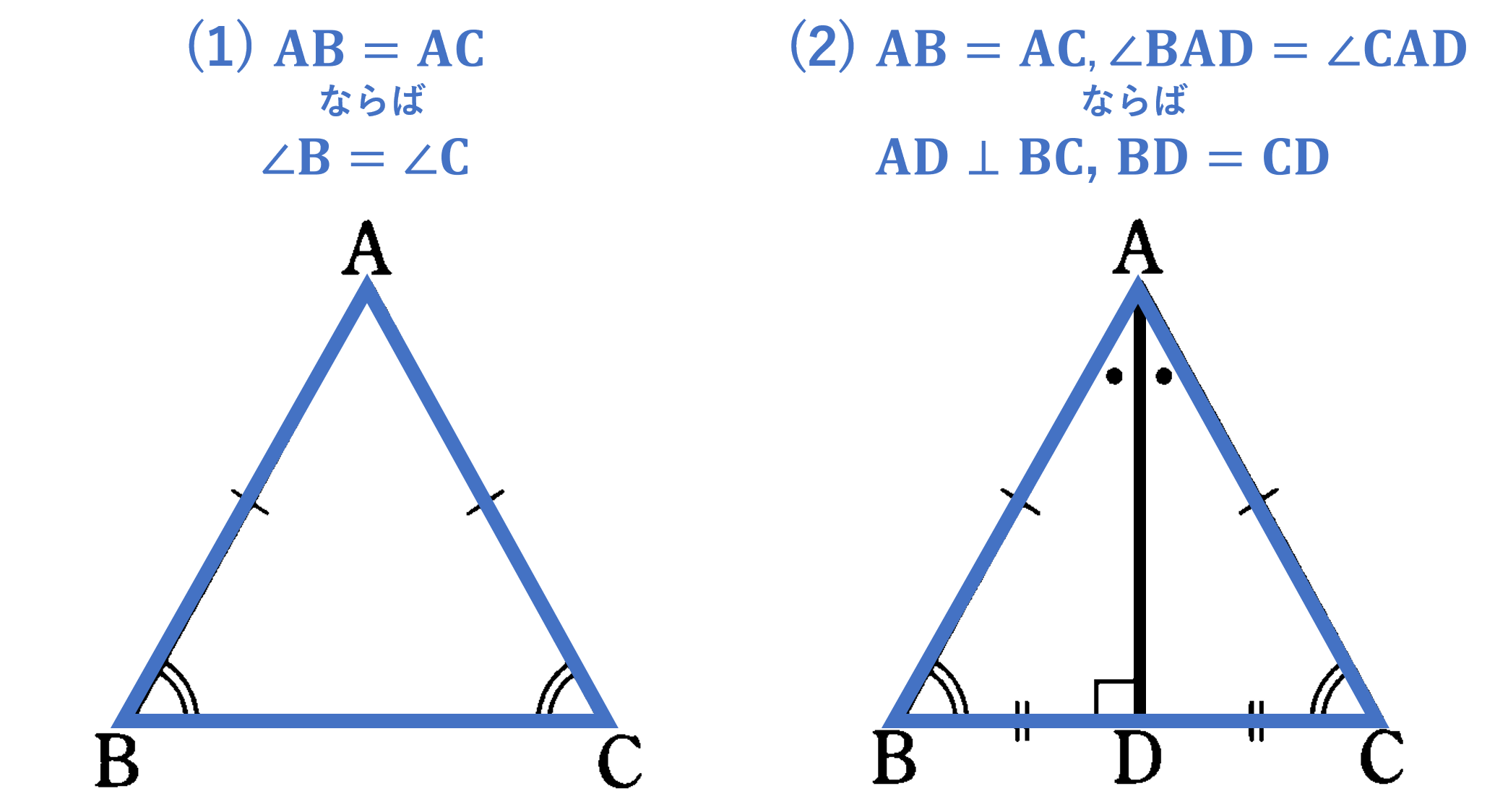



5章 三角形と四角形 タカラゼミ



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係
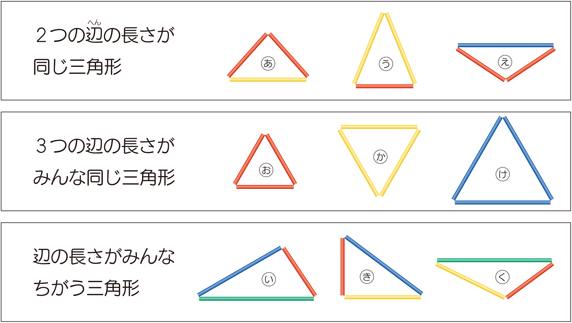



二等辺三角形と正三角形 算数用語集
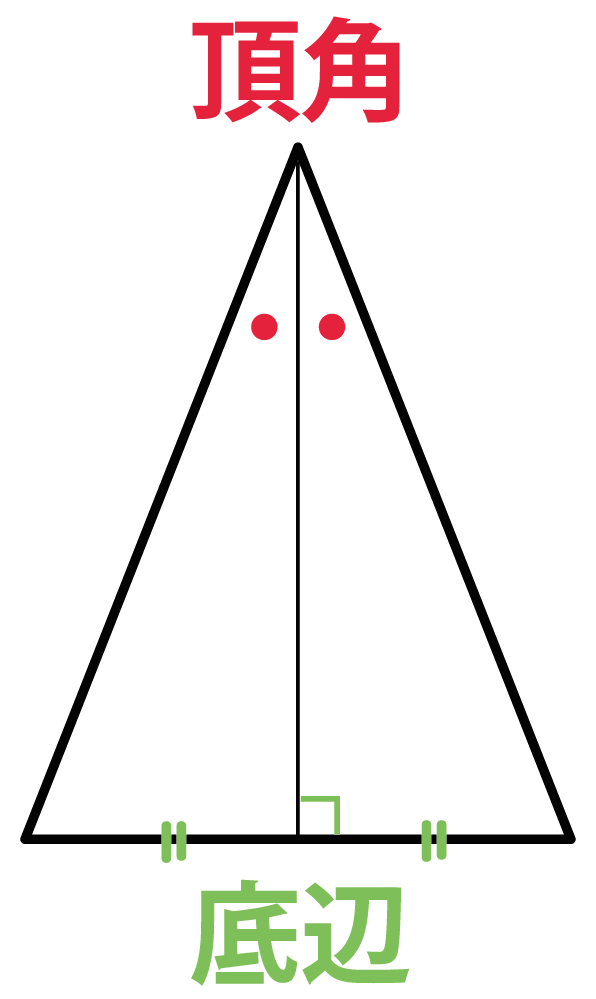



3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく




二等辺三角形の性質 定理 の逆についてです 二等辺三角形の性質 数学 教えて Goo




二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比



3年算数三角形教え方のポイント


