これは分数の通分と同じ考え方です。 この問題では(1)を4倍すると −12y ができ、(2)を3倍すると 12y ができるので、足し算により y が消去できて x だけの方程式になります。→(3) というわけで、今回の記事では 「分数を含む連立方程式の解き方」 についてイチから解説していきます。 方程式に分数が含まれている場合には 分数を無くす のがポイントとなります。両辺に10をかけて小数をなくすと21x49y=14 x3y=6の両辺に21をかけ、辺々引くと 21x63y = 126 ) 21x49y = 14 112y = 112 両辺を112で割るとy=1 y=1をx3y=6に代入すると x3=6 x=3 両辺に10をかけて小数をなくすと24x15y=33 両辺に10をかけて小数をなくすと8x25y=9

中学2年数学 分数と小数の連立方程式 勉強 Youtube スタディチューブ
分数の連立方程式の問題
分数の連立方程式の問題-となり この連立方程式の答えは 代入法の手順としては となっている式にかっこをつける かっこをつけた式をもう一方の式に代入する あとは方程式を計算 至ってシンプル! かっこをつけずに代入しちゃうと 符号ミスやかけ算忘れにつながるから連立方程式L1代入法1 2 3 4 5 連立方程式L1加減法1 2 3 4 5 6 7 8 連立方程式L2小数1 2 3 連立方程式L2分数1 2 3 4 5 6 連立方程式L3分数小数1 2 連立方程式L3分数1 2 3 4 5 6 連立A=B=C1 2 3 4 5 6 7 連立A=B=Cまとめ 連立方程式の係数1 2 3



連立方程式 代入法2 チーム エン
二元連立方程式 関数電卓が手元にないとき、面倒事を押し付けれて非常に助かります。 sqrt (値)のように使用します。 連立方程式の問題の答え合わせ。 とても便利でしたが途中の式や、分数表示ができない点が残念でした。 宿題の答え合わせに使い連立方程式 110 /41件 表示件数 5 10 30 50 100 0 1 0325 男 / 歳代 / 高校・専門・大学生・大学院生 / 非常に役に立った / 使用目的 検算 ご意見・ご感想 アルゴリズムで解いている以上,分数表示などはできないのかなと思います 10倍、100倍して小数を消せばいいよ! というわけで、今回の記事では「小数を含む連立方程式の解き方」についてイチから解説していきます。 今回の記事では以下の問題の解き方について解説していくぞ! 次の計算をしなさい。 ① ② ③ 方程式の基本
連立方程式の解につい て、変数文字の係数を 分数でなく小数で表示 したい 連立方程式を解く際に、解に含まれる文字の係数を実数で表示するようにしたいです。 以下は例です。 計算結果は以下のようコマンドウィンドウに表示されます。 この結果を 連立 方程式 答えが分数 7 Posted on November 15th, by 野球部 退 部 理由 8, カブ バッ直 リレー 26, Avenir Next フォント Adobe 6, 田中 雄士 高校 6, つむじが後ろにある 髪型 メンズ 47, 老犬 夜泣き 睡眠薬 6, 車 座席 低くする 6, スティーブ ジョブズ 大学中退 4, Activex解説 1 2 x 3 4 y2x 2 3 y= 5 18 の両辺に36をかけて分母をはらうと18x27y72x24y=10 18x27y72x24y=10を 整理して54x51y=10 1 5 x 2 5 y 1 7 x 2 7 y= 2 5 の両辺に35をかけて分母をはらうと7x14y5x10y=14 7x14y5x10y=14を 整理して6x12y=7 6x12y=7の両辺に9をかけ、辺々引くと 54x51y = 10 ) 54x108y = 63 159y = 53 両辺を159で割るとy= 1 3
連立方程式(小数係数,分数係数の問題) 例題1 次の連立方程式を解いてください. (1) (2) この問題のように係数が小数になっているときは,両辺を10倍,100倍して整数係数に直して解きます. (答案) (1)の両辺を10倍して整数係数に直す (1') (2)の両辺を100倍して整数係数に直す連立方程式(小数・分数) 連立方程式(小数・分数) 係数に小数のある連立方程式 係数に小数がある場合両辺に10,100,1000などをかけて係数を整数にすると計算しやすくなる 例 {02x03y = 13 ・・・① 005x021y =11 ・・・② ①の両辺に10をかけて、②の両辺に 中2連立方程式L1代入法1 2 3 4 5 連立方程式L1加減法1 2 3 4 5 6 7 8 連立方程式L2小数1 2 3 連立方程式L2分数1 2 3 4 5 6 連立方程式L3分数小数1 2 連立方程式L3分数1 2 3 4 5 6 連立A=B=C1 2 3 4 5 6 7 連立A=B=Cまとめ 連立方程式の係数1 2 3 x=2, y=3 x=2, y= 1 3 x=4, y=1 x=2, y= 1 2 x=1, y=3 x=4, y=3 x=1, y=4 x= 5 4, y= 3 8



Wordで問3の連立方程式を入力したいのですが 分数部分と整数部分でズレが Yahoo 知恵袋




メルカリ バラ売り可 公文 数学教材 Fとh 分数 連立方程式 応用問題 参考書 798 中古や未使用のフリマ
①分数をふくむ方程式の解き方(1) まず、下の方程式を見て下さい。 文字の項も数の項も、すべての項に分数がふくまれています。 分数をふくむ方程式をそのまま計算するのは、大変そうですよね。 じつは小数の方程式と同じように、分数をふくむ方程式も、 すべて整数の方程式 にするこY=1を9x10y=7に代入すると 9x10=7 9x=3 x= 1 3 1 3 x 9 2 y= 7 12 の両辺に12をかけて分母をはらうと4x54y=7 7 16 x 3 4 y= 13 8 の両辺に16をかけて分母をはらうと7x12y=26 4x54y=7の両辺に7をかけ、7x12y=26の両辺に4をかけ、辺々たすと 28x378y = 49 ) 28x48y = 104 330y = 55 両辺を330で割るとy= 1 6連立方程式 中学数学2元1次方程式と連立方程式 中学数学連立方程式・加減法 中学数学連立方程式・代入法 中学数学連立方程式 小数・分数;




係数が整数でない連立方程式 分数 中学生 数学のノート Clear




連立方程式を小学生に教える
連立方程式L1代入法1 2 3 4 5 連立方程式L1加減法1 2 3 4 5 6 7 8 連立方程式L2小数1 2 3 連立方程式L2分数1 2 3 4 5 6 連立方程式L3分数小数1 2 連立方程式L3分数1 2 3 4 5 6 連立A=B=C1 2 3 4 5 6 7 連立A=B=Cまとめ 連立方程式の係数1 2 3 x=2, y=2 x=2, y=1 x=3, y=2 x=1, y=1 x=2, y=3 x=4, y=3 x=2, y=4 x=5, y=3置き換えによる連立方程式 解説 のように分母にx,yなどの文字を持つ方程式は,分数でなくす(分母を払う)ためにxyを両辺に掛けると, となり,xyは文字を2つ含む2次の項なので1次方程式ではありません。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru




分数が含まれている連立方程式の解き方 全国 中学数学ができるようになるブログ




分数と小数の連立方程式の解き方が分かりません 教えてください Clear
この形の方程式を解くとき,普通の方程式を解くときの 「移項」のような変形をしにくい ので,解き方のコツを覚えておくとよいでしょう. 〇「 A=B=C 」というのは,「 A=B かつ B=C 」を省略的に書いたものです.だから,「 A=B=C 」という方程式が与えられ分数が含まれている連立方程式の解き方! こんにちは! 平均点すら取れないけど100点を取ってみたい中学生に数学を教えている東亜紗美です! 数学の授業 を 個別指導 しています! ! みんなだったら、どう解くかな? あとは、xの値も求めるために、 ①、②、②'のどの式にy=2を代入 しても解けるよ! 名古屋市で対面授業を個別で受けることができます連立方程式(分数6) 連立方程式を解け 5x3 2 4y2 3 = 17 3 15x8y=9 4x1 3 3y5 4 = 1 3 3x9y=15 2x1 3 7y4 3 =1 2x5y=18 5x4 6 2y1 3 =12 9x7y=9 3x7 2 2y5 9 = 11 18 5x32y=7 9x1 4 5y3 6 = 25 4 3x7y=33 8x7y=12 5x3 12 7y4 16 = 17 12 2x5y=5 9x11 10 5y3 6 = 27 5 3x2y=9 4x3 7 3y4 5 = 24 7 2x4y=12 2x3 9 3y11 8 =12 2x1 6



中学の数学 分数の連立方程式の解き方について質問です の両辺に15 Yahoo 知恵袋




数学 時短演習cote
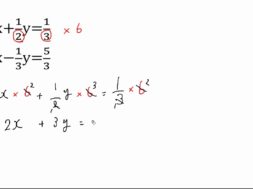
解説 1 4 x 1 2 y2x 2 3 y= 13 12 の両辺に12をかけて分母をはらうと3x6y24x8y=13 3x6y24x8y=13を 整理して27x14y=13 2 3 x 1 3 y 1 5 x 2 5 y= 8 5 の両辺に15をかけて分母をはらうと10x5y3x6y=24 10x5y3x6y=24を 整理して13x11y=24 27x14y=13の両辺に11をかけ、13x11y=24の両辺に14をかけ、辺々たすと 297x154y = 143 ) 1x154y = 336下の式の 分数は先に整理 しよう。 1/2は邪魔だから、2をかけて消したい よね。 同じように、 1/3には3をかけたい 。 だから、 2×3の6を両辺にかければ、2つの分数は整理できる ね。 (上の式) x+y=50 (下の式)×6 3x+2y=180 あとは、 上の式に2をかけてyの係数を合わせれば解いていくことができる ね。 ④の答え係数に分数のある連立方程式 係数に分数がある場合、両辺に分母の公倍数をかけて係数を整数にすると計算しやすくなる 必ずしも最小公倍数にこだわらなくてもよい 例 { 1 2 x 1 3 y = 2 ・・・① 2 5 x 2 3 y = 2 5 ・・・② ①の両辺に6をかけて、②の両辺に15をかけて係数を整数にする { 3x2y = 12 ・・・①' 6x10y = 6 ・・・②' ①'×2②' 6x4y = 24 ) 6x10y = 6 6y = 18 y = 3




連立方程式 分数を含む計算の解き方をイチから解説 Youtube




分数と小数の連立方程式の解き方が分かりません 教えてください Clear
2 連立非線形微分方程式 この節では,非線形微分方程式を考察する. 21 複素数を用いた解法 2年前のノート1では,次の連立非線形微分方程式が可積分であること,また,複素数を使うと簡単に積 分できることを示している.ここでは,その内容のポイントを振り返ろう.x=x(t)とy=y(t)に関する連 これで連立方程式の解である $$(x, y) = (5, 2)$$ がゲットできたね。 まとめ:分数の連立方程式はまずは「分母を払う」から 連立方程式に分数があるとむずかしそうだよね?? だけど、 やることは案外すくないよ。 ただ、 分母をはらう



2 7e といてみよう 分数や少数のある連立方程式 ホンわか先生




連立方程式 割合の問題 おっかぁ Note




世界一わかりやすい数学問題集中2 2章 連立方程式
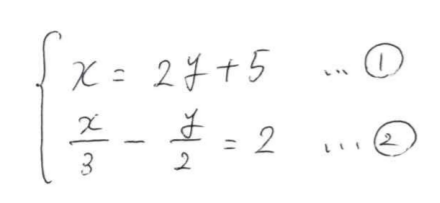



分数が含まれている連立方程式の解き方 全国 中学数学ができるようになるブログ




中2数学 連立方程式 小数 分数を含む連立方程式 Youtube




中学数学2年 連立方程式 代入法 受験の月




Akiya Su Auf Twitter 数学 連立方程式 濃度 昨日の答えと難題 分数や小数がある方程式の解き方も確認しておこう 中学数学 連立方程式 濃度




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者



連立方程式 代入法2 チーム エン




方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題




方程式の解き方まとめ 中3生は必見 これで受験を乗り切ろう 中学数学 理科の学習まとめサイト




たけのこ塾 Na Twitteru 中2数学 今回は 連立方程式の計算問題 を作成しました カッコや分数を含むと連立方程式の解き方を しっかり復習しておきましょう 詳しくは画像の解説をご覧下さい 勉強垢 中2 数学 連立方程式 Youtube T Co




分数の方程式の問題 解き方のコツは両辺に数をかけて分母を消せ 中学や高校の数学の計算問題
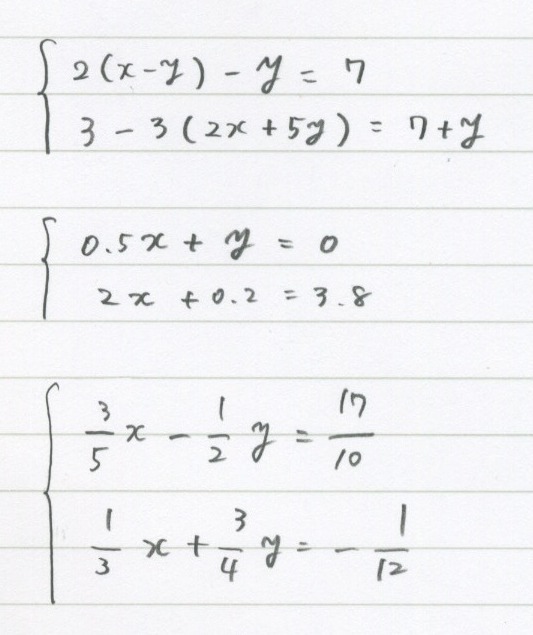



5 2 連立方程式 かっこや分数小数はもうできる 勉強できようサイト




中学2年数学 分数と小数の連立方程式 勉強 Youtube スタディチューブ




連立方程式の代入法 簡単な問題で やり方をわかりやすく紹介 中学や高校の数学の計算問題




分数をふくむ連立方程式 Youtube




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




中学数学 連立方程式 の効果的な教え方 小数 分数問題




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




分数の連立方程式 解き方は両辺に数をかけて分母を消すんだ 中学や高校の数学の計算問題




方程式練習問題 連立方程式の文章問題 道のり 速さ 時間 方程式の解き方まとめサイト




連立方程式 分母の数が大きい場合の計算 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ




中学2年数学 分数と小数の連立方程式 Youtube



中学二年です 分母に文字のある連立方程式の解き方を教えてくださ Yahoo 知恵袋



中1 一次方程式の分数は整数になおそう 中学数学の方程式 中間 期末テスト 高校入試対策




教えて下さい 連立方程式が分数の場合はどうやって解けばいいんですか Clear



2 27第2章いろいろな連立方程式 分数を含む連立方程式 プログラミングの雫
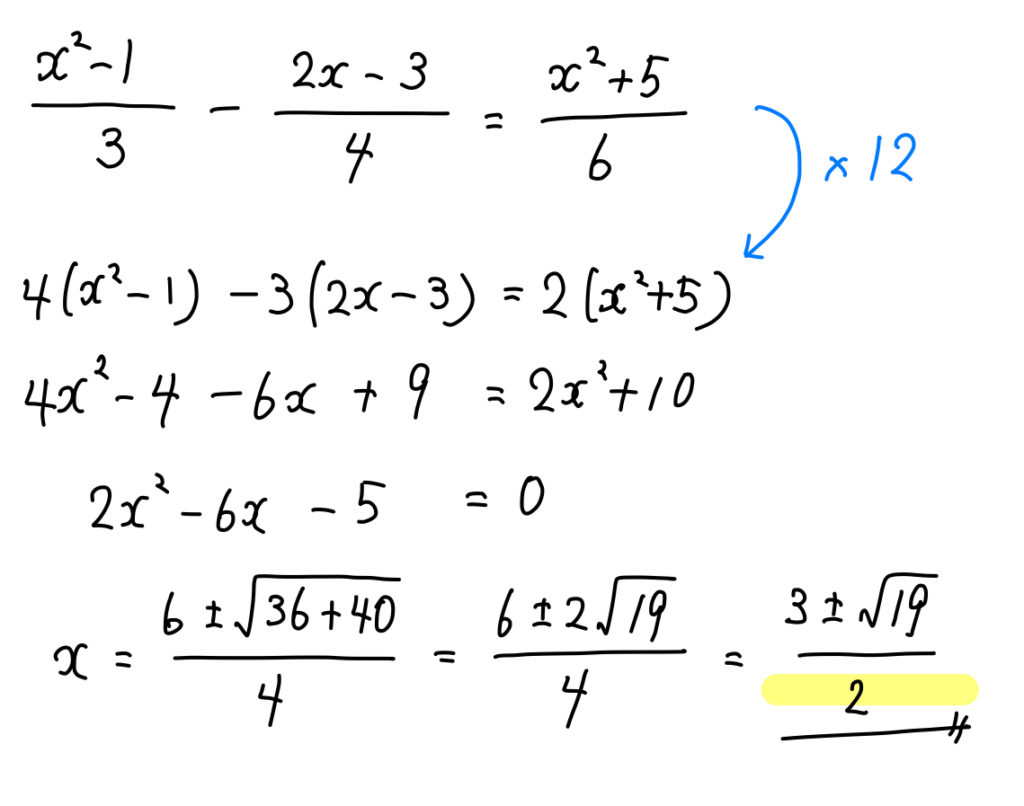



分数 小数 ルートを含む二次方程式の解き方まとめ 数スタ



連立方程式とは チーム エン



1




たけのこ塾 中2数学 今回は 連立方程式の計算問題 を作成しました カッコや分数を含むと連立方程式の解き方を しっかり復習しておきましょう 詳しくは画像の解説をご覧下さい 勉強垢 中2 数学 連立方程式 Youtube T Co Waess9diai
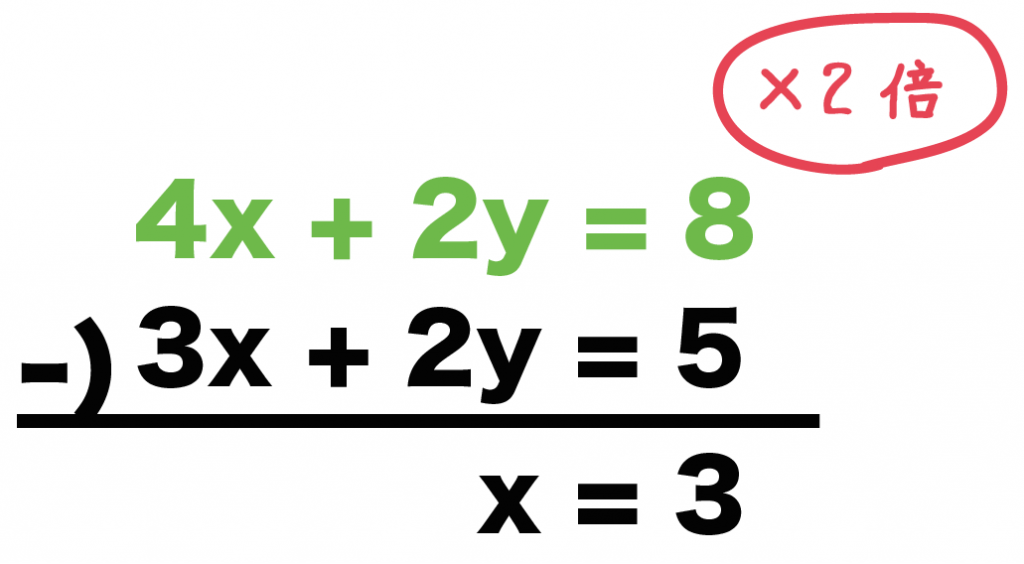



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




中学数学 連立方程式 文章題の解き方 割合の問題




中学1年生 数学 無料問題集 分数の一次方程式 おかわりドリル




ロイヤリティフリー分数 の 連立 方程式 解き方 最高のぬりえ




3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく



分数のある連立方程式の代入法の解き方




分数形の不定方程式の解き方をイチから解説 数スタ



連立方程式です 中2このプリントのこの問題がわかりません 答えはもら Yahoo 知恵袋



連立 方程式 計算 分数



Iseqi Pukiwiki




中2数学 カッコ 分数を含む連立方程式 例題編 映像授業のtry It トライイット




例題付き 連立方程式の解き方と失敗しないコツ



連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス
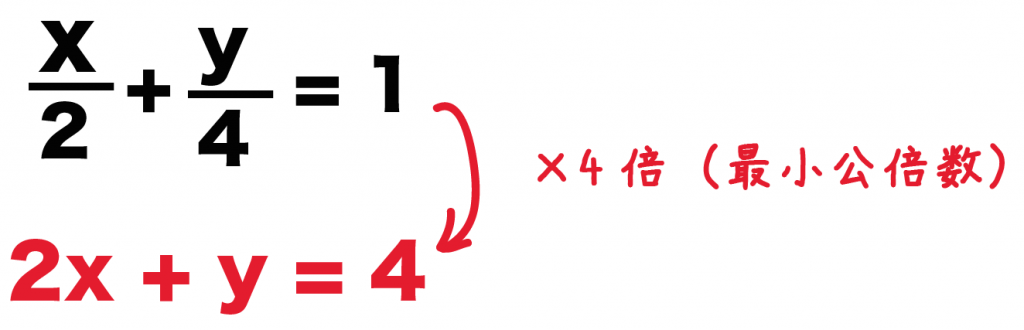



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




このような文字が分母の連立方程式の計算方法教えてください Clear




中学2年生 数学 いろいろな連立方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




分数の連立方程式 Youtube




小数の連立方程式 Youtube




中学数学2年 いろいろな連立方程式 係数が小数 係数が分数 A B C型 受験の月




3つの連立方程式の問題 解き方はこのようにすればバッチリだ 中学や高校の数学の計算問題




一次方程式の解の求め方 数学fun




連立方程式 分数ありバージョン 苦手な数学を簡単に




連立方程式 いろいろな計算 無料で使える中学学習プリント




中学2年生 数学 いろいろな連立方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Q Tbn And9gcqs7b6jmju9we92tekzdua7ji8dogsp5 Nep Gxayd Boghf0vd Usqp Cau
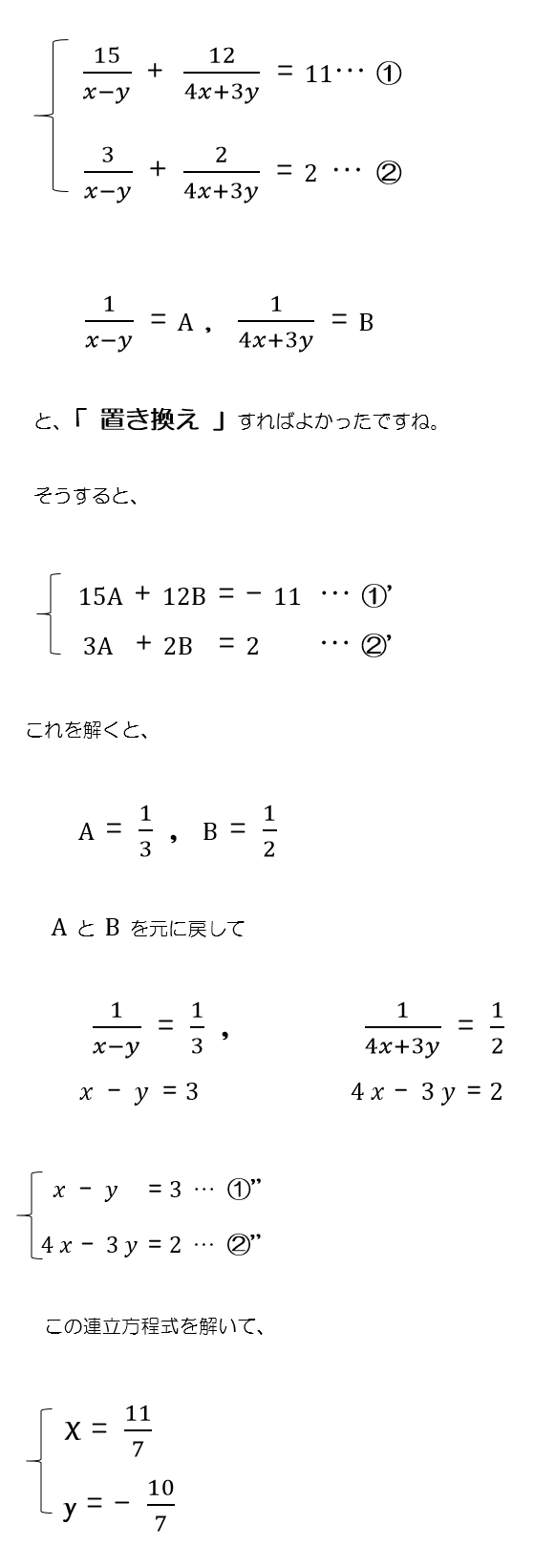



なるほど数学コラム 中学編 8 分母に文字がある連立方程式 を解こう Katekyo学院 教室で個別指導塾ならkatekyo学院 自宅でプロ家庭教師は福島県家庭教師協会 県内各地域で受講可能 福島 郡山 白河 会津 喜多方 いわき 相馬



連立方程式の分数の回答お願いします こうだと思います 矢印の Yahoo 知恵袋




中3数学 分数を含む二次方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




連立方程式の加減法の解き方をマスターしたい方は見てください 中学や高校の数学の計算問題




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者



中2数学 02 9 分数の連立方程式 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト



1




連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト
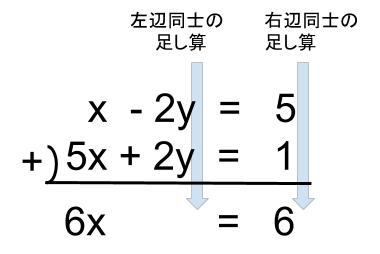



中学数学 連立方程式 小数 分数 中学数学の無料オンライン学習サイトchu Su



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料
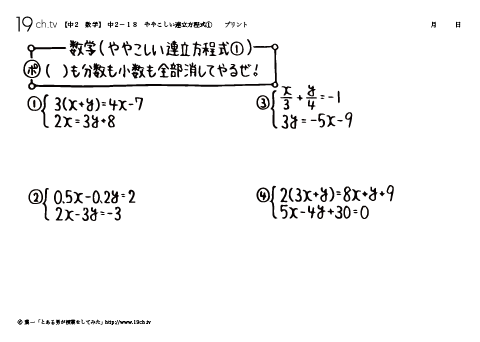



中学2年の数学 動画 ややこしい連立方程式 の問題 19ch




分数を含む方程式 Youtube




高校数学で学習する連立方程式の解き方まとめ 数スタ




分数の連立方程式の解き方が分からないので教えてください お願いします Clear




連立方程式の解き方 係数に分数がふくまれる場合 Youtube




分数の連立方程式の解き方を教えてください で何を考えたら答えを導き出せるのか教えて Clear
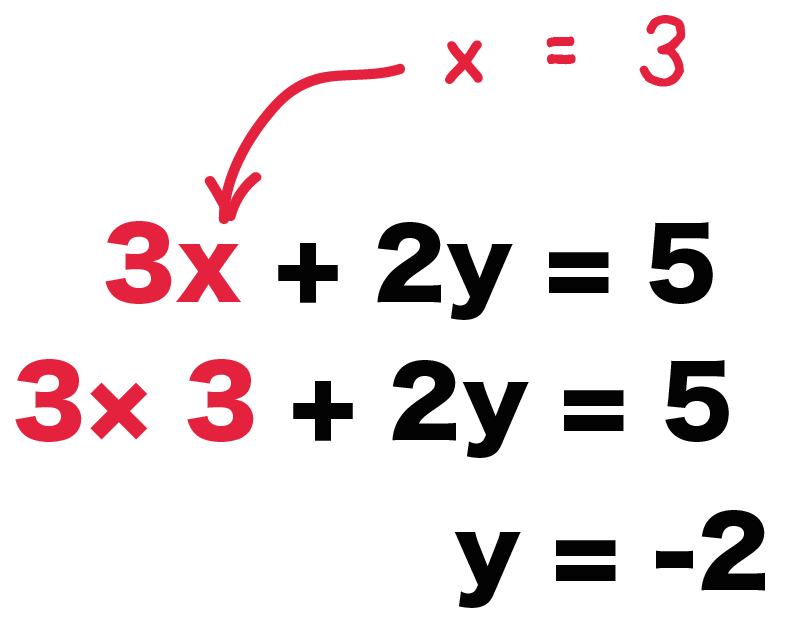



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく



3



連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料




鉄則12 不等式 分数不等式 無理不等式 寺田の数学合格鉄則96に関するメモ




中学1年生 数学 無料問題集 分数の正の数 負の数の加法 足し算 おかわりドリル




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学




置き換えによる連立方程式 まなびの学園
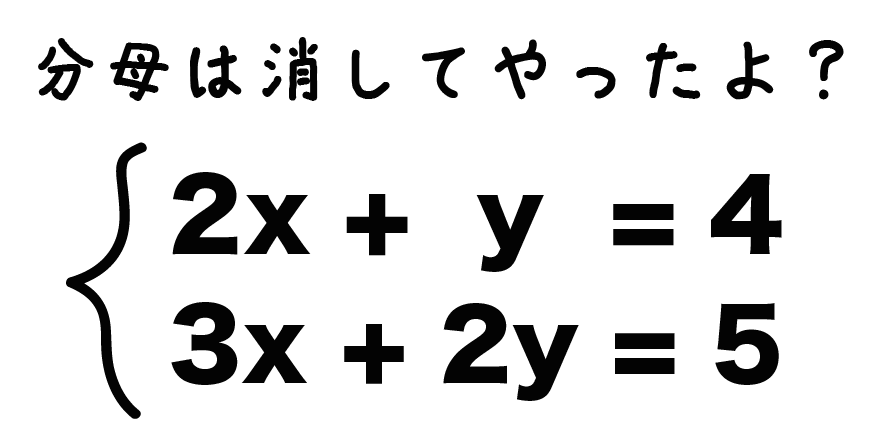



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット



連立方程式の小数と分数の混ざった式について この問題が解 Yahoo 知恵袋



分数の 連立方程式 を整数に直すために 3をかけているのかが良くわか Yahoo 知恵袋




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




連立方程式の解き方と交点の座標の求め方 数学の偏差値を上げて合格を目指す




画像の 3 のような分数と小数の混ざった連立方程式がわかりません 解 数学 教えて Goo




連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




小数の連立方程式の解き方 両辺を10倍や100倍しよう 中学や高校の数学の計算問題




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者
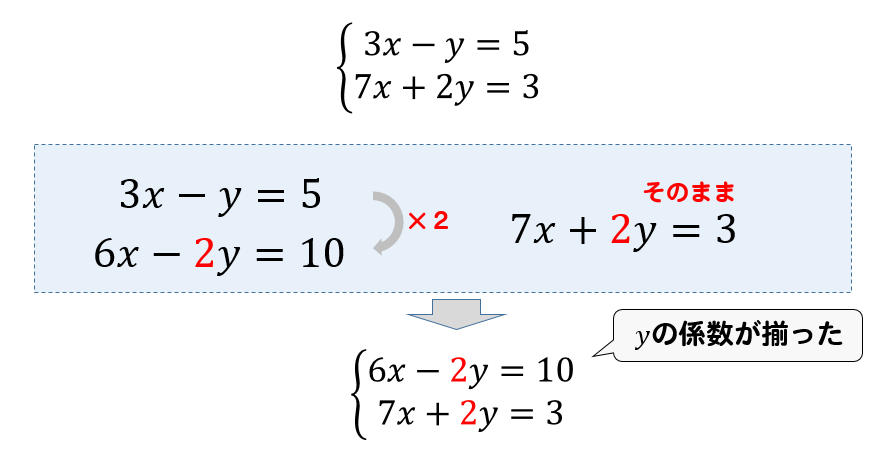



連立方程式 加減法を使った問題の解き方は やり方をイチから解説 方程式の解き方まとめサイト




中学2年 連立方程式の計算 第3講 清水塾


