教え方3 「速さ」と「時間」を使って、「道のり」の求め方をとらえさせます。 問題 白黒ねこは、秒速10m走ります。 5秒走ったら何m(道のり)進みますか? イラスト提供元 下はそのイメージです このことから、道のりを求める式は 道のり=速さ×時間・平均の意味とその求め方,用 い方 使った速さの比べ方 ・単位量当たりの大きさの考え とその用い方 (時速・分速・秒速) 直方体や立方体の体積 四角形と三角形の面積 ・簡単な場合の比例 ・単位量当たりの大きさの考えを ・速さの意味とその求め方 ・速さに関する公式 間と道のりの関係 「道のり」を求めたい場合には、この表の「み」の部分を隠すと こんな感じで、道のりを求めるための式を導くことができます。 他も同様。 ゆい ちょー便利だね♪ 一次方程式の利用道のりを求める文章題の解き方 例題① 往復する時間差 A町とB町を往復するのに、行きは分速1mの

数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく
道のり 求め方
道のり 求め方-池1周分の道のりを①で割る 次に、2人が同じ方向に進む場合 上で紹介した2人が追いつくときのように、差を考えながら解いていきます。 2人の進んだ道のりの差が池1周分である2400mになれば、追いついたことになります。地図をなぞって距離を計算 よかった。 たすかりました。 ランニングコースの距離を測りました。 実際に計測してみたかった! 良かった! ただ屈折点の数が限られるので、増えたらもっと重宝します! ありがとうございます! 朝のランニング距離を




数と式 一次不等式を扱った応用問題を解いてみよう その3 道のり 速さ 時間 日々是鍛錬 ひびこれたんれん
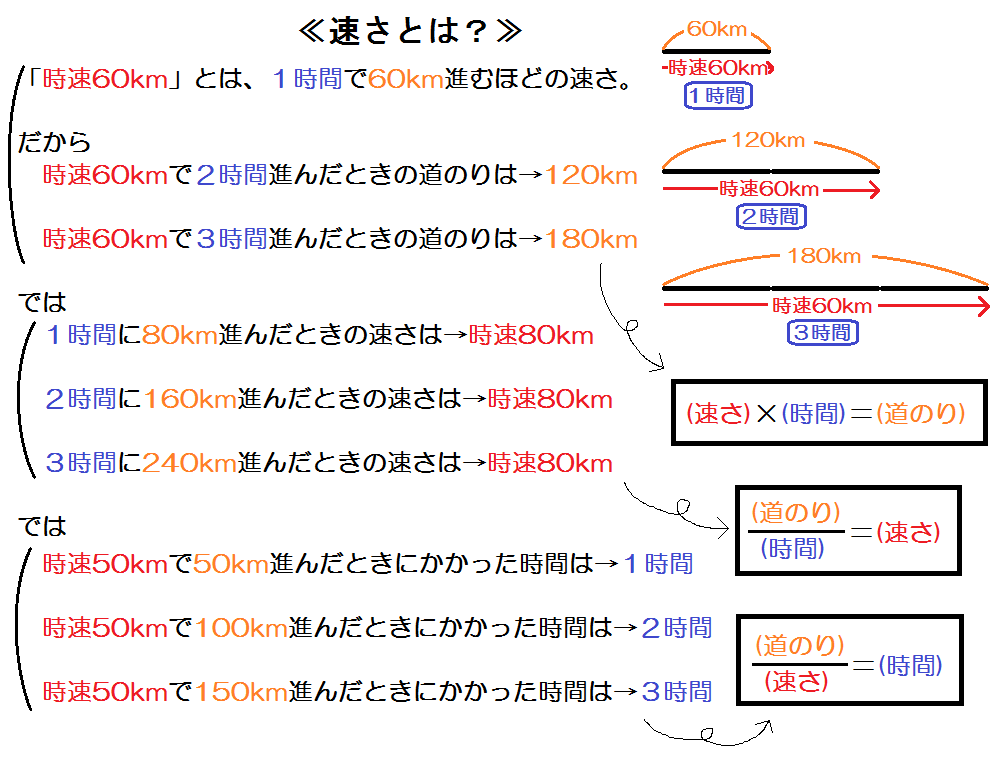
めあて 道のりや速さを使って、時間の求め方を説明しよう。 問題1 自動車が高速道路を時速80km で走っています。 標示板 名古屋 240km 静岡 360km あと、何時間で名古屋に着きますか。 い 静岡までの時間を求めましょう。と求められます。 (3) (2) と同様に余事象の考え方を用います。まずは × の部分を通る最短経路の総数を求めますが,異なるのは (2) ではある点を通る最短経路の総数だったのに対し, こちらはある道を通る最短経路の総数について考えるということです。 速さ (km/h) = 道のり (km) ÷ 時間 (h) 時間 (h) = 道のり (km) ÷ 速さ (km/h)
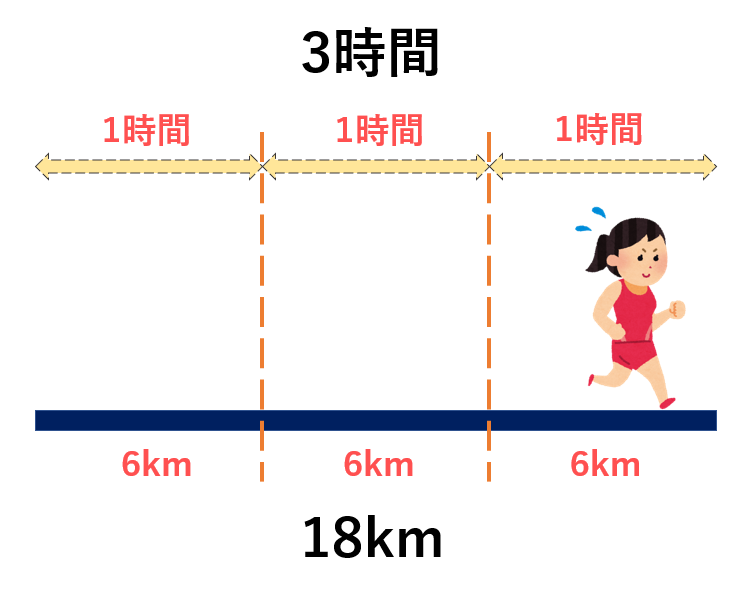
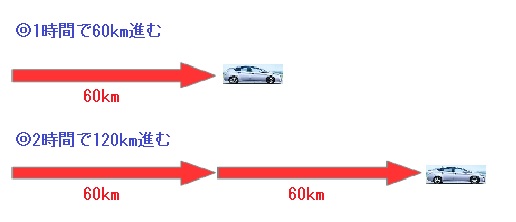
距離の求め方 時速4㎞で2時間歩いた場合の距離を考えると、1時間で4㎞歩いて2時間かかったので、時速4㎞という「速さ」に2時間という「時間」をかける(速さ×時間)ことで、実際に歩いた「距離」の8㎞を求めることができます。 これは「距離=速さ×時間」という公式です。 時間の求め方教え方4 「道のり」と「速さ」がわかっているときの「時間」の求め方をとらえさせます。 問題 時速80㎞で走るバスが、240㎞進むには、なん時間かかりますか? アニメを見て かんがえましょう。 と、走る距離が1時間ごとに80kmずつふえていきますね。 答えは 3時間です。 動画作成協力・・動く1歩で1段か2段を上るとき,9段の階段を上る上り方は全部で何通りあるか。 解答 この方法で n n n 段の階段を上る方法を a n a_n a n 通りとする。 a 1 = 1, a 2 = 2 a_1=1,\a_2=2 a 1 = 1, a 2 = 2 , a n 2 = a n 1 a n (n ≥ 1) a_{n2}=a_{n1}a_n\(n\geq 1) a n 2 = a n 1 a n (n ≥ 1) を使って順々に a n a_n a n を求めていく
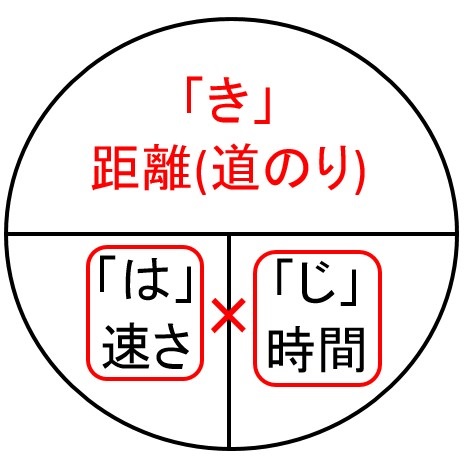
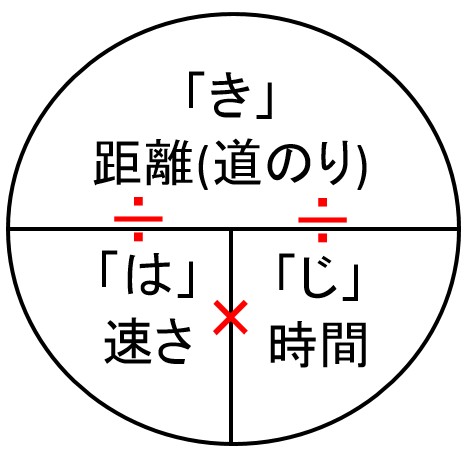
道のりの求め方解答 速さの求め方はこちらからごらんください。 sukusapokidshateblojp 時間の求め方はこちらからご覧ください。 sukusapokidshateblojp finesukusapo 1252 Tweet 関連記事 小6算数「時間の求め方」に無料プリントがつきました。 算数の無料動画が好評の「すくサポキッズ 数iii積分区分求積法の考え方と使い方を整理する 数Ⅱ指数対数なぜ対数というものがあるのか? さて 『はじき』の法則ですが図に書いてみました。 一目瞭然です! 簡単すぎて一度覚えたらきっと忘れないでしょう。 円の中にある横の棒は 「÷」 円の中にある縦の棒は 「×」 すると簡単に公式に当てはまります。 距離=速さ×時間 速さ=距離÷




速さと時間から道のりを求める問題 家庭学習レシピ




往復の平均の速さ 間違えずに求められますか
道のりの求め方を見る前に、速さの基本を押さえておきましょう。 速さの単位の意味が分かればこれ以降も理解できると思いますが、ちょっと知識があやしそうな場合は1度復習してみてください。 速さの単元の要になります。 ・速さの単位、時速、分速、秒速の意味はこちら 速さの単位公式 時間 = 道のり÷速さ 一郎君がA町からB町までを自転車で往復した。行きは分速150mで、帰りは毎分1mで走ったら、往復で45分かかった。A町からB町までは何mあるか。 A町からB町までの道のりをxmとする 行きにかかった時間は x 150, 帰りは x 1 である。往復の平均時速を求めなさい。ただし、行きと帰りの 走行距離(道のり)に差はないものとする。 いかがでしょうか? こんなこと、考えていませんか? ① 2つの平均なんだから、行きと帰りを 足して2で割れば簡単に求まる!




問4の解き方が分かりません どのようにして時間を求めるのか教えてください Clear




中2数学 連立方程式の文章題 速さ 練習編 映像授業のtry It トライイット
すでにそれぞれの道のりは 弟50 (x +8) 兄70 x と表しているので、この式に先ほど求めた x =を代入してやれば求めることができます。求める走行距離 (m) 走行速度(時速)×1000÷60÷60×走行時間(秒)= m40道のりの求め方速さ・時間・道のりの計算 スポンサーリンク ここで2点注意です。 一つ目は「道のり」と「距離」の違いです。 これは僕も教えてもらったことなんですけど、距離はaからbまでの最短の長さを指し示す言葉。 道のりは、駅から家まで等の長さを指し示す言葉として



はじきの法則とは 距離 道のり 速さ 時間を計算する公式について とはとは Net




速さと時間から道のりを求める問題 家庭学習レシピ
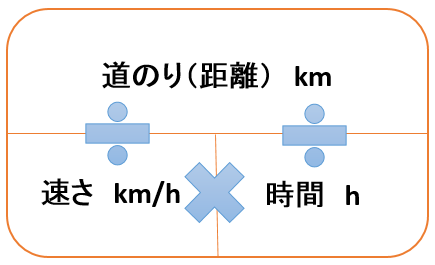
AからBまでの道のりは何km?ここから先は簡単な計算です。 小学校で習った公式 道のり = 速さ × 時間 で求められるからです。 (式) a / 60 × b = ab / 60 (答) ab / 60 km このようになりますね! <まとめ> 相性のよい単位を押さえましょう。 距離(道のり) = 速度(速さ) x 時間 速度(速さ) = 距離(道のり) ÷ 時間 時間 = 距離(道のり) ÷ 速度(速さ) となることを表は示しています。もちろんどれか1つを覚えて、あとは、計算式を求めたいものに変換していく方法もあります。例えば"距離 = 速度 x 時間スマートフォン のためウォーキングをしているが時速7キロ歩行が良いと聞き、現在歩いている5キロの道のりを何分で歩けば良いか出したかったため。 7 0133 歳代 / 会社員・公務員 / 非常に役に立った / 使用目的 アメリカテキサス州ヒューストン郊外の住宅地




道のりときょり 低学年の無料学習ドリル




速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい
道のり=速さ×時間 速さ=道のり÷時間 時間=道のり÷速さ ただこれらはわざわざ覚える必要はなく、簡単に導出可能です。 たとえば 割合 の時と同じように長方形に当てはめれば、3つの公式は自然と導けます。 割合の3つの公式の覚え方と使い方時間の求め方(問題) 学習する学年:小学生 問題 時間を求める解き方を覚えて計算力をつける為に、次の時間を求める計算をしましょう。 答えは、時、分、秒を求めるので問題をよく読んでから計算してください。 問1. 8km/hの速さで16kmの道のりを走った。 走り終わるのに何時間かかり速さの求め方 時間は,次のように考えて求めます。 速さと道のりから時間を求めるには,進むのに かかる時間を 時間として,道のりを求める公式を 使って, にあてはまる数を求めます。 例 時速50km で走る自動車が150km 進むのに かかる時間 50* =150 =150/50 = 3




数的処理 超 基礎講座 道のり 速さ 時間 平均の速さの求め方 高卒程度公務員試験対策 数的推理 Youtube
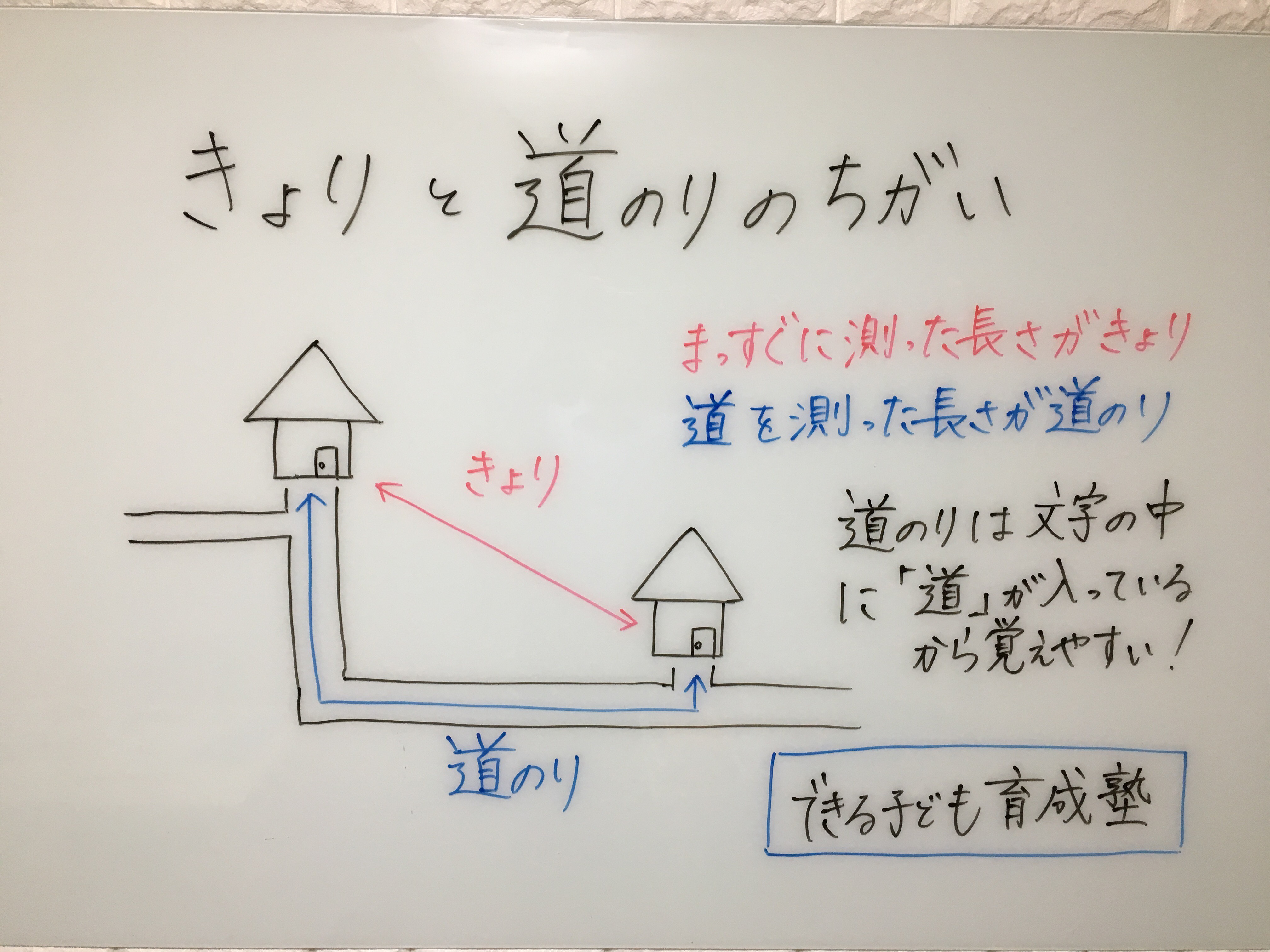



距離と道のりの違い 小学3年生の算数の問題 小岩 個別指導 元小学校教師が教える個別指導塾 できる子ども育成塾 小岩 篠崎の小学生専門 国語と算数の苦手を克服
速さと道のりをもとに、時間の求め方をとらえることができる。 5.単元指導計画 時 学習活動及び内容 1 こみ具合等、数直線を用いながら単位量あたりの大きさで比べるという既習の学びをふり返る。 2 進んだ道のりとかかった時間をもとに、数直線を用いながら1分間あたりに進む道のり学習する学年:小学生 1.時間の単位と求め方 時間は算数の授業で学習する以外でも毎日の日常生活の中で時計の時間を読む時に使っているので馴染みがあるものです。 時間を読む時は、時、分、秒を使って読むと思いますが、時(h)、分(min)、秒(s)とは何のことかわかりますか?平均の求め方 です。そもそも速さというもの自体が「進んだ道のり÷かかった時間」によって計算しているので、平均を表しているのと同じはずです。 例えばこれが、女子4人のテストの平均90点、男子5人のテストの平均72点だったとして、全体の平均を求めるときはどうするでしょうか



暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社




数と式 一次不等式を扱った応用問題を解いてみよう その3 道のり 速さ 時間 日々是鍛錬 ひびこれたんれん
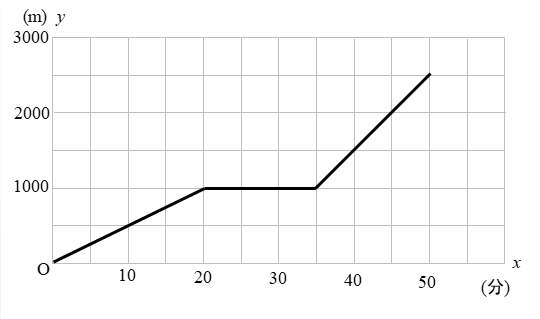
00導入速さ、時間、道のりの勉強を始める前に 平均と合計 0702速さの求め方と単位 速さ、距離、時間の関係 秒速と計算方法(求め方)と、小学生でもパッと出せる考え方を解説します こんにちは。 大阪で、行列の出来るラーメン店「人類みな麺類」など、6つのラーメンブランドを運営している松村貴大( @jinrui_mina_men )と申します。道のりの求め方はイメージしやすいと思います。 公式にすると、 道のり=速さ×時間 速さの求め方 「道のり」と「時間」がわかっていれば、「速さ」は簡単に求められます。次の例題を使って考えてみましょう。 (例題2) 家から学校までの道のりは480mです。今日は遅刻ギリギリで、走って




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく




距離と道のり違いとは 小3算数に出てくる道のりの意味 Ruruのあれこれ日記
道のりを求める公式を理解し、それを適用して道のりを求めることができる。 (2) 授業の視点 して有道のりを求める方法を数直線に表して考える活動は、道のりの求め方を理解する手立てと 効であったか。 (3) 本時の展開 過 学 程 習 内 容 時求め方を、道のりを求める式から考える。 技② (観察・発言・ノート) 2 速さとグラフ(1) 6 ・速さの適用問題を表にまとめた り、グラフに表したりして解く。 ・時間と道のりの関係を表にまとめたり、グ ラフに表したりする 30 第6学年 算数科学習指導案 日 時 平成23年9月8日(木



数と式 一次不等式を扱った応用問題を解いてみよう その3 道のり 速さ 時間 日々是鍛錬 ひびこれたんれん




速さと時間から道のりを求める問題 家庭学習レシピ




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生



はじきの法則とは 距離 道のり 速さ 時間を計算する公式について とはとは Net
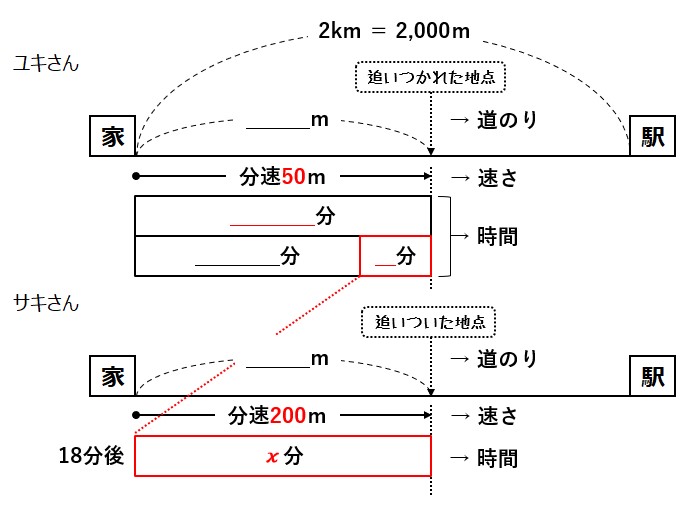



わかる 中学数学 一次方程式の利用 文章題 道のり 速さ 時間の問題 を丁寧解説
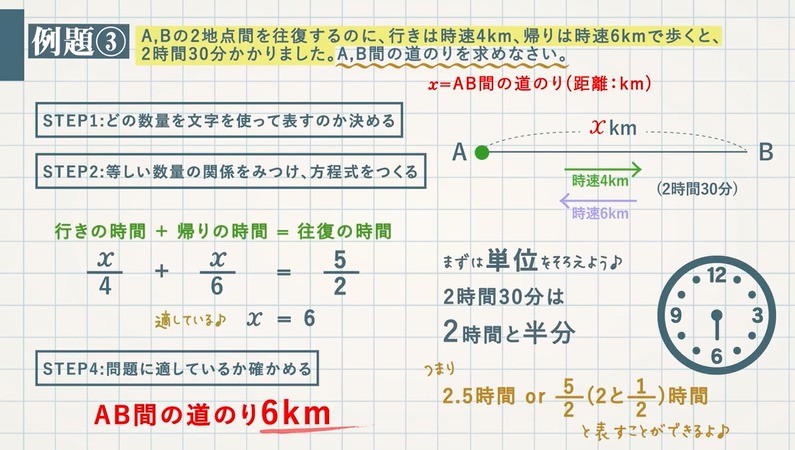



方程式の利用 文章題 距離 速さ 時間 教遊者




中学数学1年 1次方程式の利用 速さ 時間 道のり 受験の月




小学6年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり
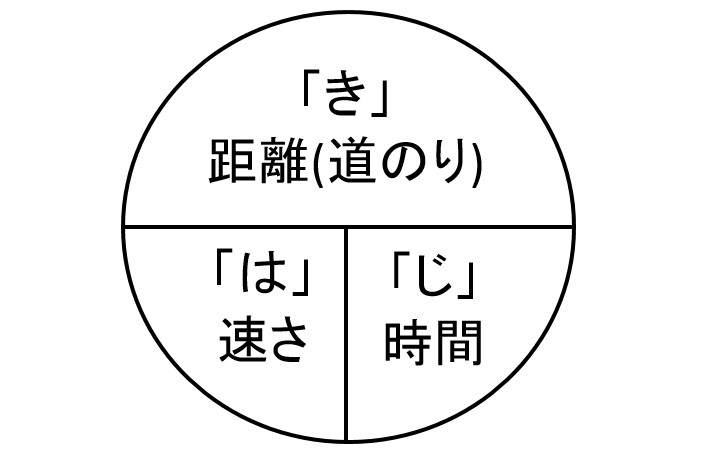



はじきの法則とは 距離 道のり 速さ 時間を計算する公式について とはとは Net



小中学生 道のり 速さ 時間の公式を理解しよう 偏差値40プログラマー
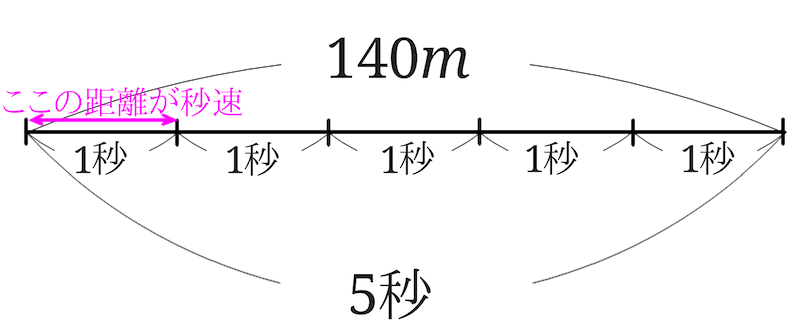



速さの求め方を時速 分速 秒速ごとに解説 みけねこ小学校
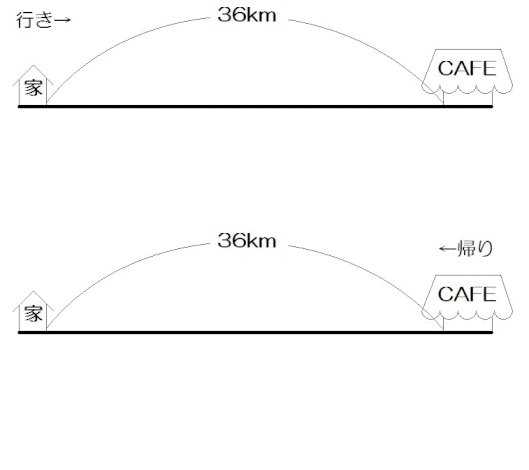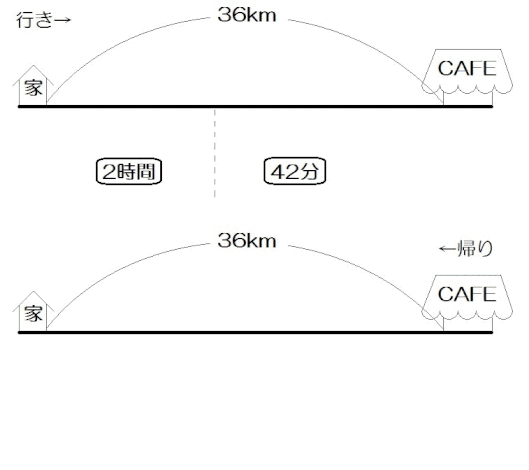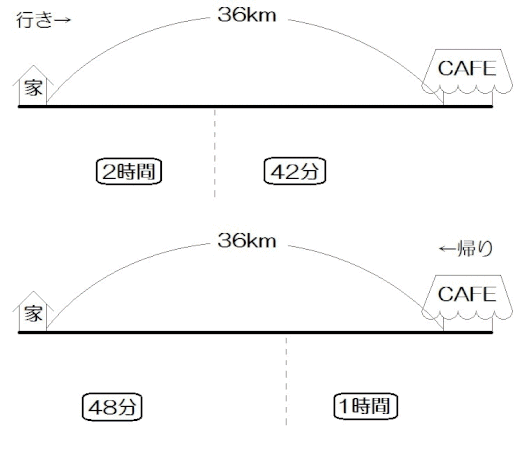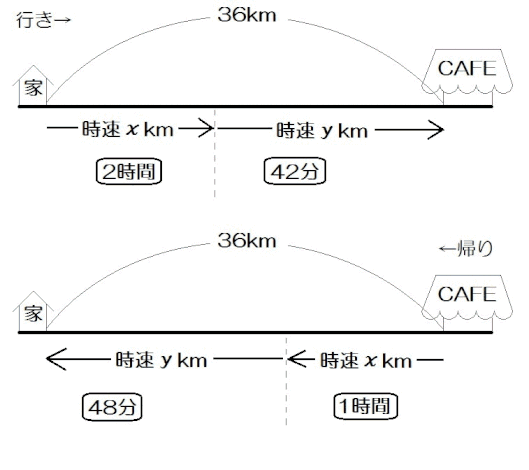



中学数学 連立方程式 文章題の解き方 速さ 時間 道のり問題




速度問題 速さ 道のり 時間 小学6年生 算数



1




はじきの計算 例題を使って問題を解説 速さ 距離 時間を求める方法は 数スタ




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun




往復の平均の速さ 間違えずに求められますか




道のり 速 さ の 求め 方 3171
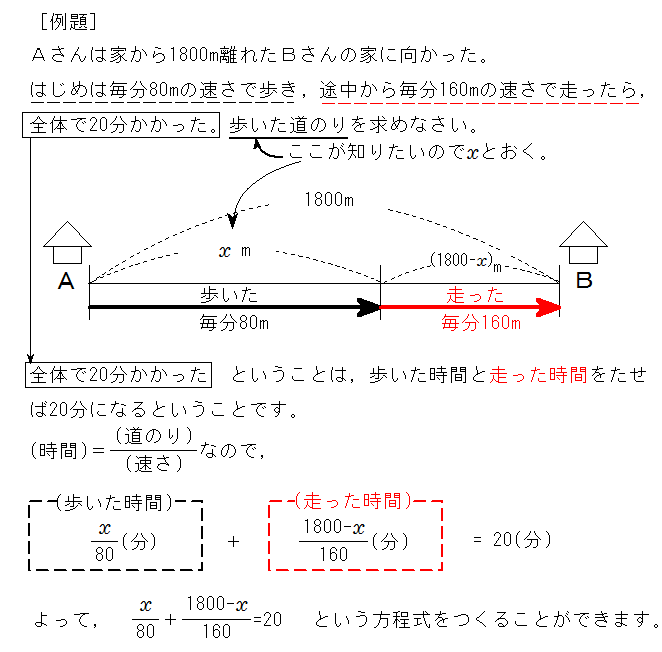



方程式 途中で速さが変わる問題の解き方 中学数学 定期テスト対策サイト




道のりの求め方 Youtube
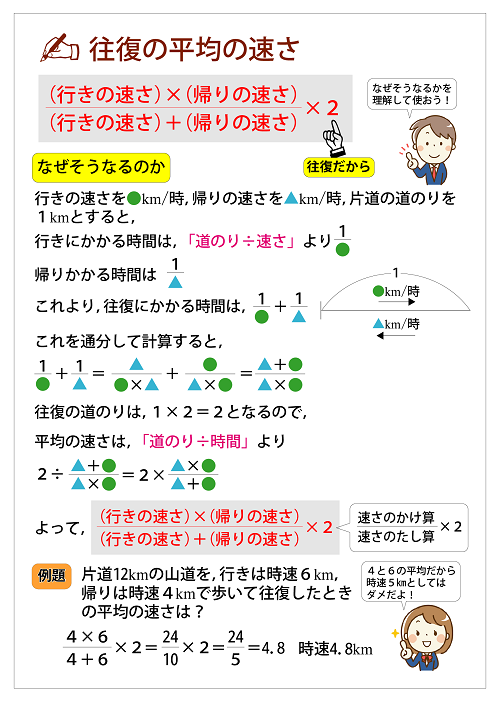



往復の平均の速さに関する公式のカードを作りました 恋する中高一貫校 適性検査 徹底攻略



は じ き は悪魔の公式 算数が苦手な子には文章題はこう見えている 江南の塾 ネクサス 勉強のやり方専門塾 小中高一貫の少人数個別指導塾



一次関数の利用 追いつく速さの文章問題を解説 数スタ
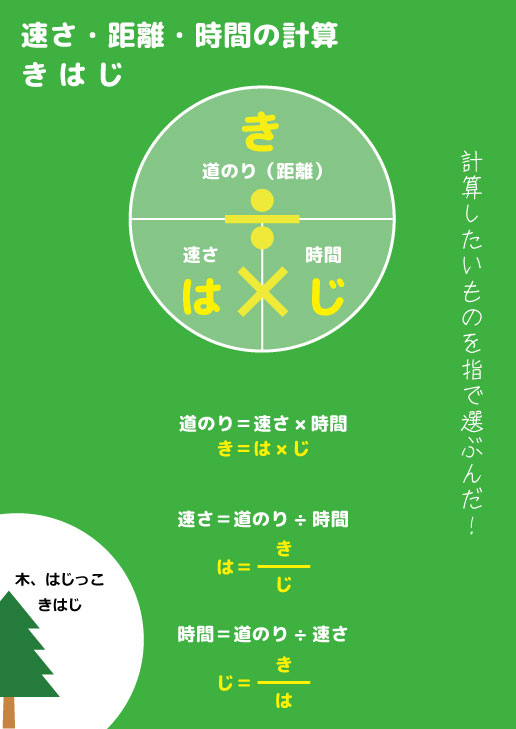



6年生の算数 速さ 時間 距離の式をイメージで覚える 算数検定7級




すきるまドリル 小学6年生 算数 速さ 無料学習プリント すきるまドリル 無料学習プリント



1




速さ 分速と秒速 数学の記録



中1数学方程式の利用ってとこの方程式の文章問題なんですけど道のりを求める文 Yahoo 知恵袋
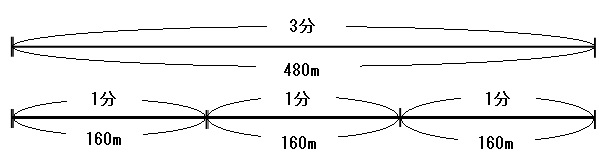



速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい
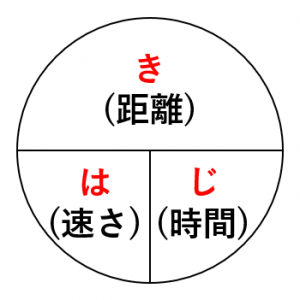



速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun



1
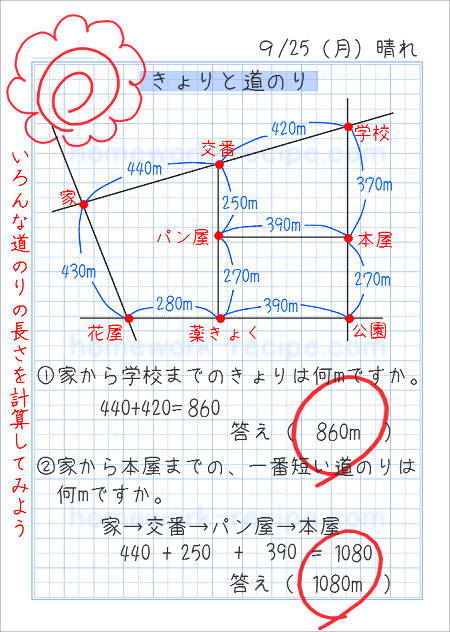



きょりと道のりの練習問題 家庭学習レシピ
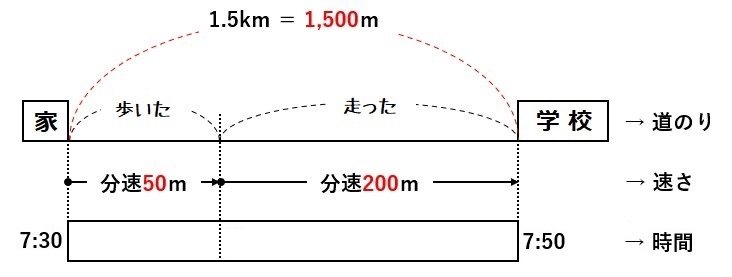



納得 中学数学 一次方程式の利用 文章題 道のり 速さ 時間 かわる 問題 徹底解説




連立方程式の利用の問題の解き方 はやさの問題 3 現役塾講師のわかりやすい中学数学の解き方
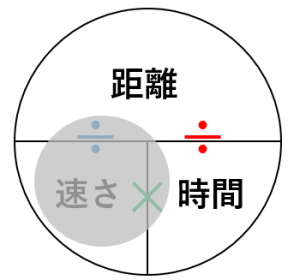



速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学
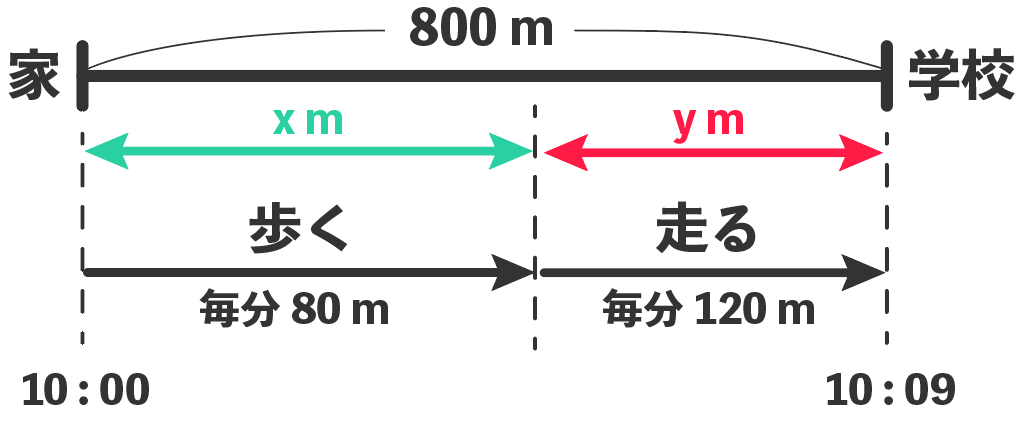



連立方程式の利用 速さ 道のり 時間の文章問題の解き方 Qikeru 学びを楽しくわかりやすく




速さ 時速 数学の記録




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく
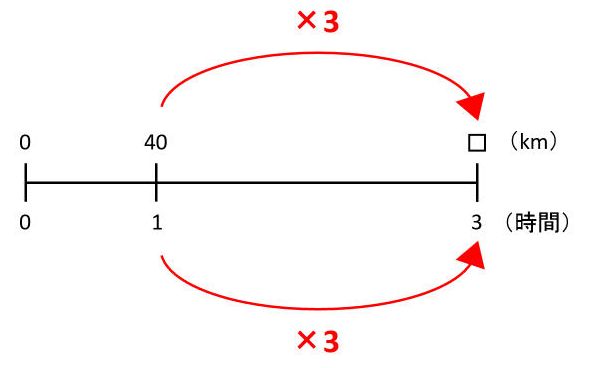



速さ 線分図 面積図 ダイヤグラムがあれば みはじ は要らない みみずく戦略室
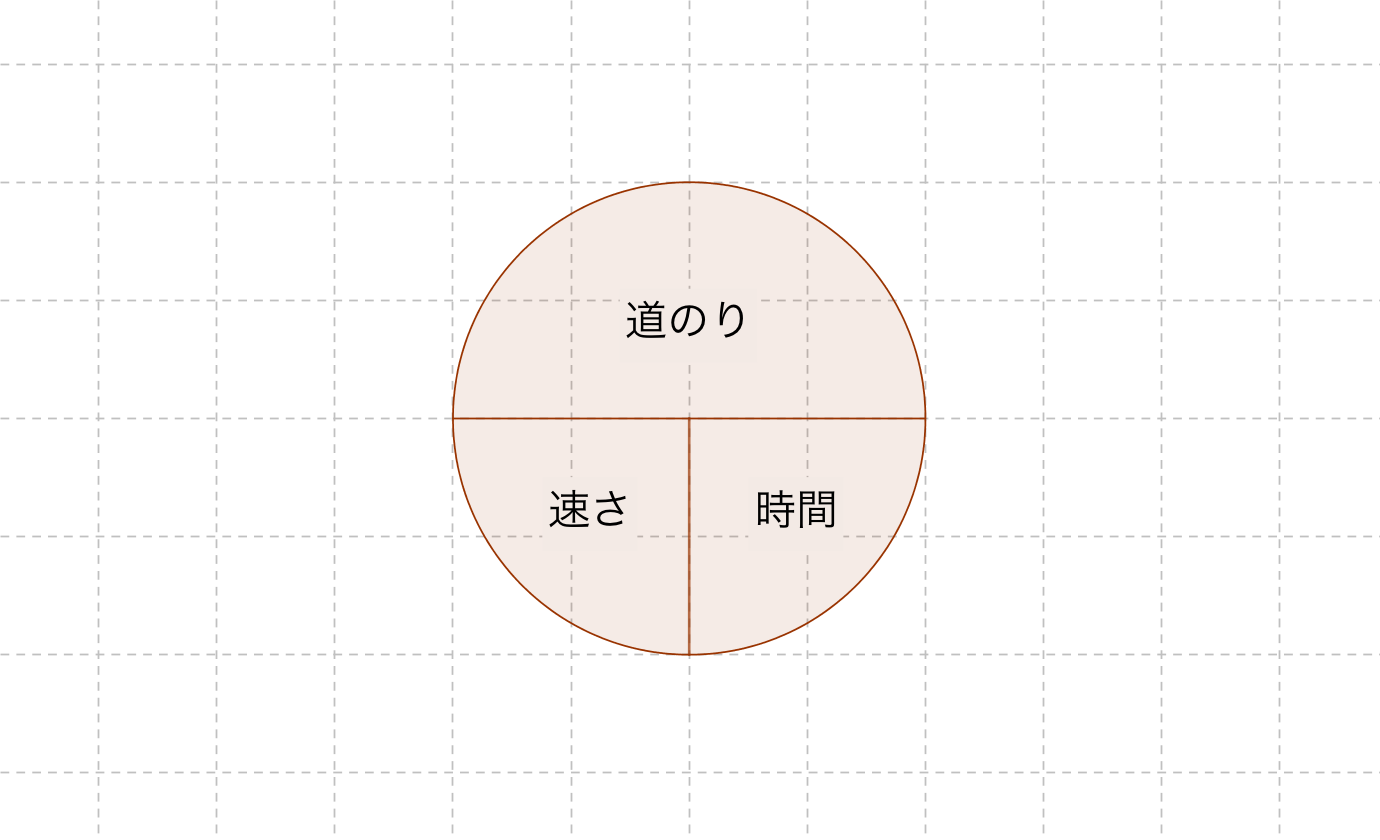



速さの公式 道のり 時間 算数の公式
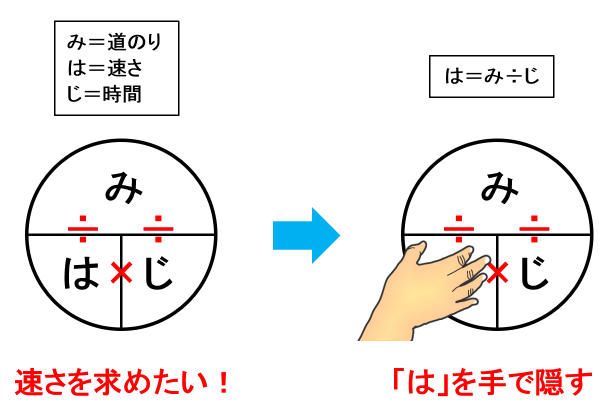



速さ 線分図 面積図 ダイヤグラムがあれば みはじ は要らない みみずく戦略室




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり




速さについての問題には 様々なパターンがあります その中でも基本となる 時速 分速 秒速の換算の問題 道のりとかかった時間から速さを求める問題を 自主学習として解いてみましょう 学習ノート 学習 一生懸命に勉強する



海図の問題を覚えよう 距離 速度 時間の計算



道のりlの求め方が分からないので 途中式もよろしくお願いします Yahoo 知恵袋




暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社
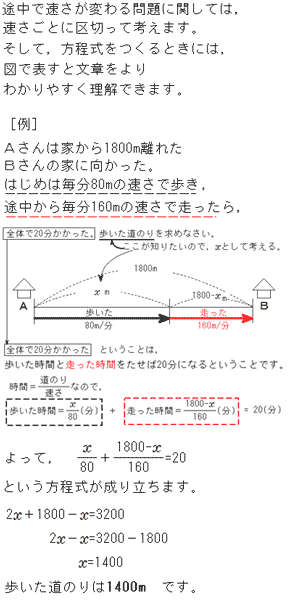



方程式 途中で速さが変わる問題の解き方 中学生からの勉強質問 数学 進研ゼミ中学講座




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




小6 算数 小6 22 速さの表し方 練習編 Youtube
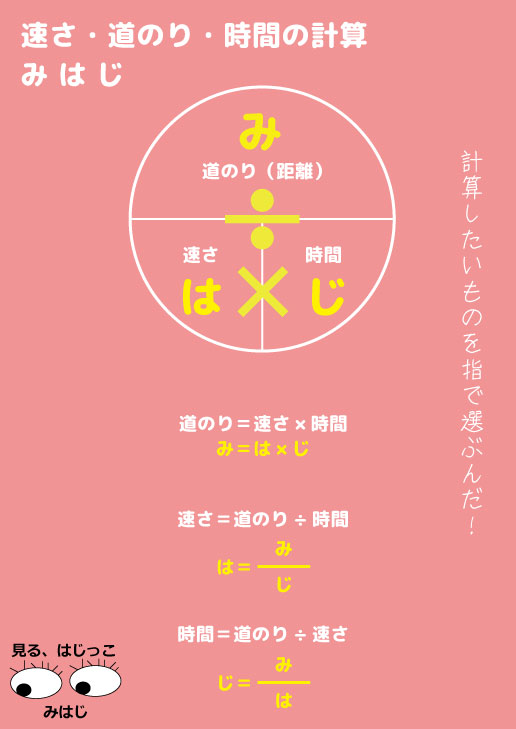



6年生の算数 速さ 時間 距離の式をイメージで覚える 算数検定7級




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生



Studydoctor速度から道のりや変量の求め方 高校数学 Studydoctor




中2数学 連立方程式 速さの問題 よくわかりません 教えていただきたいです Clear



道のりの求め方 速さ 時間 道のりの計算




速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい



道のり 速さ 時間の求め方を教えてください 求め方 など考えなく Yahoo 知恵袋
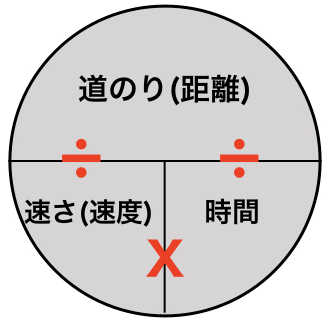



速度計算 速度 距離 時間と速さ 道のり 時間の覚え方攻略 Landgather




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく




速さや時間の単位が揃っていない道のりの求め方 みけねこ小学校




文字式 速さの問題をわかりやすく解く方法 数スタ




連立方程式の速さの問題です 教えてください Clear




中学数学2年 連立方程式の利用 速さ 時間 道のり 受験の月
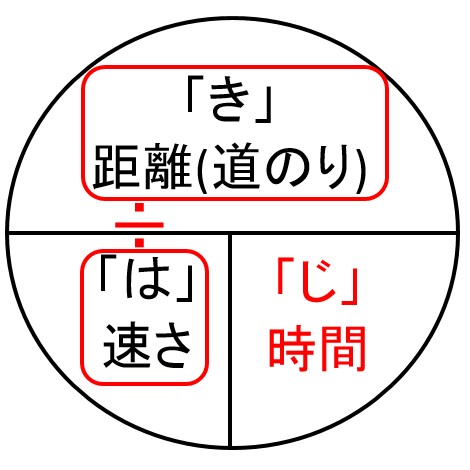



はじきの法則とは 距離 道のり 速さ 時間を計算する公式について とはとは Net




小6 算数 小6 21 速さの表し方 基本編 Youtube




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生



1




6年生算数ドリル 速さ




方程式の利用の道のりの求め方を教えてください Clear



速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun



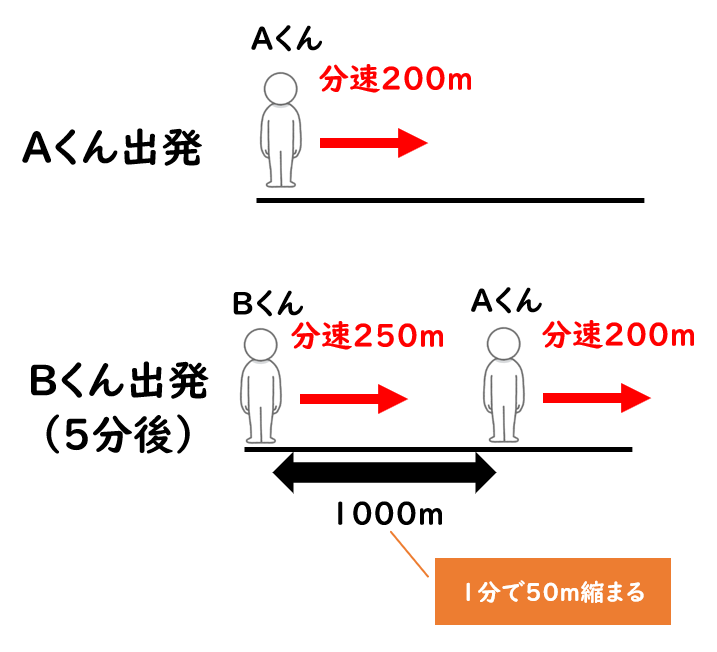
速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい
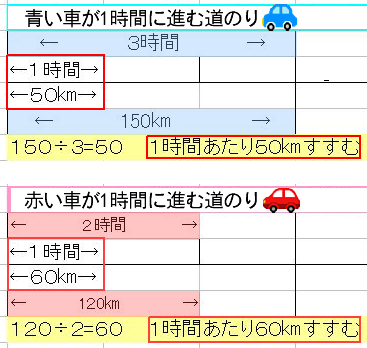



5年算数速さ 教え方のポイント




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく




速さ の公式と問題の解き方のポイント 小学生に教えるための解説 数学fun
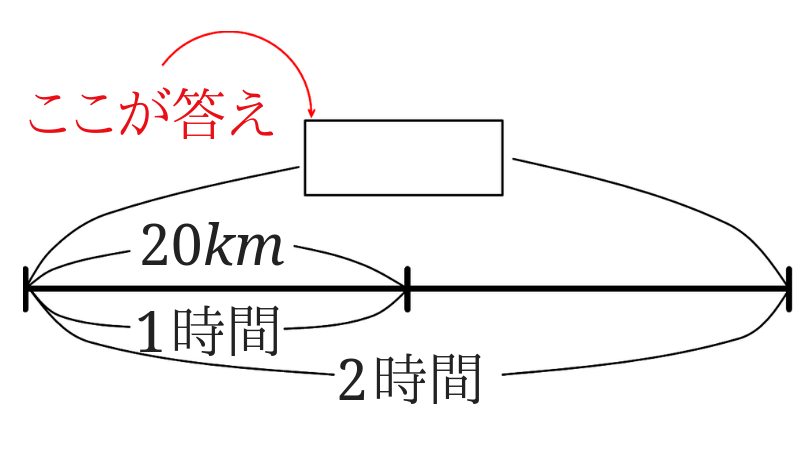



速さの公式に頼らない道のりの求め方ができるようになろう みけねこ小学校
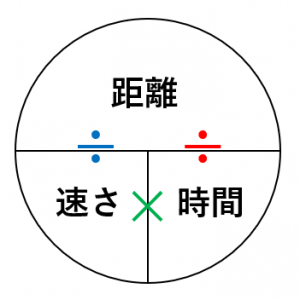



速さ 時間 距離を計算する公式の使い方と覚え方 具体例で学ぶ数学
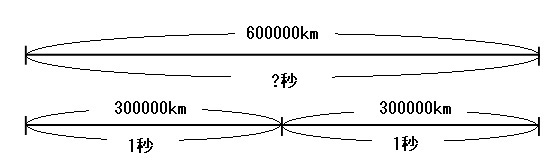



速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい




速さの公式に頼らない道のりの求め方ができるようになろう みけねこ小学校
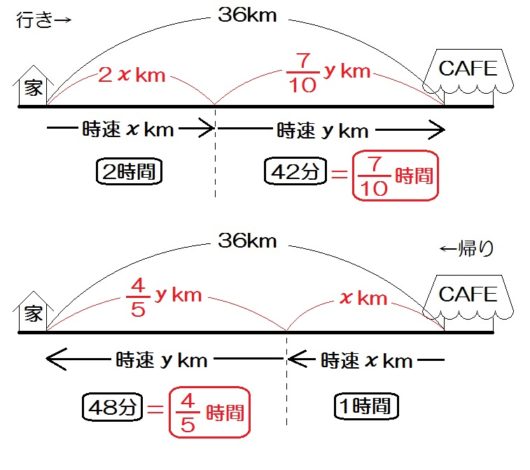



中学数学 連立方程式 文章題の解き方 速さ 時間 道のり問題




小6 算数 小6 道のり 速さ 時間 Youtube
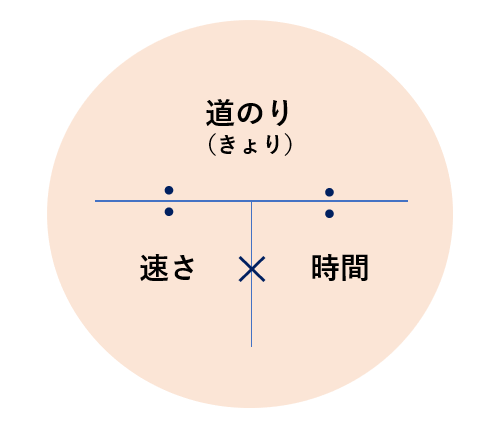



暗記嫌いのための速度算 速さ 時間 道のりの関係 数学 統計教室の和から株式会社




時間の求め方 Youtube




小学6年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生



中学数学 1次方程式 文章題の解き方 速さ 時間 道のり



Www City Omura Nagasaki Jp Kurogisyo Kyoiku Documents Sansuupowerup6 Pdf


